 |
Законы распределения непрерывных случайных величин.
|
|
|
|
Министерство образования и науки Украины
Приднепровская государственная академия
Строительства и архитектуры
Кафедра прикладной математики
Статистический анализ
Методические указания к изучению
Теории математической обработки результатов
Геодезических измерений
и выполнению курсовой работы
Днепропетровск
Статистичний аналіз. Методичні вказівки до вивчення Теорії м атематичної обробки результатів геодезичних вимірювань і виконання курсової роботи. Для студентів будівельного факультету / Укладач Цибрій Л.В. Дніпропетровськ: ПДАБА, 2008. – 50 с. рос. мовою.
Укладач Цибрій Л.В., к.ф.-м.н., доцент
Відповідальний за випуск: Єршова Н.М., д.т.н.,проф., зав.каф.прикладної
математики ПДАБА
Рецензент: Скрипник В.П., к.ф.-м.н.,
доцент
Затверджено
на засіданні кафедри
прикладної математики
9.04.2008р.
протокол №9.
Затверджено
на засіданні
Методичної ради ПДАБА
Содержание
Введение 4
I. Статистический анализ
1.1. Основные понятия выборочного метода 6
1.2. Законы распределения непрерывных случайных величин.
Нормальный закон распределения 7
1.3. Оценка параметров распределения 10
1.4. Статистическая проверка гипотез 12
II. Корреляционный и регрессионный анализ
2.1. Система случайных величин 15
2.2. Основы корреляционного анализа 17
2.3. Регрессия. Линии среднеквадратической регрессии 19
2.4. Выборочное уравнение регрессии 20
2.5. Основы дисперсионного анализа 22
2.6. Нелинейная корреляционная связь 23
III. Многомерный статистический анализ 25
3.1. Основные характеристики многомерной генеральной
совокупности 26
3.2. Множественная корреляция 27
|
|
|
3.3. Множественное уравнение регрессии 30
IV. Статистический анализ в Excel
4.1. Очистка информация от засорения 31
4.2 Проверка закона распределения 33
4.3. Корреляционный анализ 35
4.4. Регрессионный анализ двумерной модели 36
4.5. Регрессионный анализ трехмерной модели 41
V. Содержание и объем курсовой работы 46
VI. Литература 47
Приложение 48
Введение
В основе теории математической обработки результатов геодезических измерений лежат понятия теории вероятностей и методы математической статистики. Введение понятия случайной погрешности измерений позволяет рассматривать ее как случайную величину, а закон ее распределения и числовые характеристики определять в соответствии с законами теории вероятностей.
В процессе обработки результатов прямых равноточных и неравноточных измерений одной и той же геодезической величины производится точечная и интервальная оценки их параметров распределения. Однако, многие одномерные величины в геодезии, как, например, длины сторон треугольников триангуляции и полигонометрии, широты, долготы пунктов Лапласа, непосредственно не измеряются, а их значения находят из вычислений по соответствующим формулам. Каждая такая зависимость представляет собой функцию случайных величин. Основным методом исследования при этом является метод математического моделирования, базирующийся на использовании средств компьютерной техники. Под математическим моделированием понимают способ исследования различных явлений, процессов путем исследования явлений, имеющих разное физическое содержание, но описываемых одинаковыми математическими соотношениями.
Математической моделью реальной зависимости называется ее описание на каком-либо формальном языке, позволяющее выводить суждения о некоторых чертах поведения этой зависимой величины при помощи формальных процедур. Математическая модель может представлять собой функциональные зависимости или графики, уравнения. Другими словами, математическая модель – это отражение оригинала в виде функций, уравнений, неравенств, цифр и т.д. Математическое моделирование – мощный метод познания, а также прогнозирования и управления. Математическое моделирование занимает ведущее место среди других методов исследования, особенно благодаря компьютерной технике, возможности которой позволяют исследование поведения системы случайных величин осуществлять с помощью машинного эксперимента. Математической моделью распределения результатов измерений служит многомерная нормально распределенная случайная величина. Важнейшей характеристикой связи между случайными величинами многомерной системы является корреляционный момент. Сама связь описывается функцией регрессии. Оценки коэффициента и функции регрессии по статистическим данным являются задачей корреляционно-регрессионного анализа.
|
|
|
С развитием науки и техники, в частности самой геодезии и информационных технологий, повышается точность измерений и совершенствуются методы их математической обработки. Однако, в измерениях возможны просчеты, или грубые ошибки (выбросы). Для обнаружения их следует применять методы статистического анализа.
Многомерный статистический анализ выполняется средствами надстройки Excel «Пакет анализа».
Для успешного выполнения задания приводятся необходимые сведения из теории вероятностей и математической статистики, и устанавливается связь между параметрами теоретического и статистического распределения изучаемых факторных и результативных признаков.
I.Статистический анализ
Современная математическая статистика – это наука о принятии решений в условиях неопределенности. Основная цель математической статистики: обосновать выводы о массовых явлениях и процессах по данным наблюдений над ними или по результатам экспериментов. Эти статистические выводы относятся только к общим характеристикам этого явления, а не к отдельным испытаниям, и только в предположении постоянства условий, их порождающих.
Две основные задачи математической статистики:
|
|
|
Ø указать способы сбора и группировки статистических сведений (результатов экспериментов или наблюдений);
Ø разработать методы анализа статистических данных (оценка характеристик распределения, проверка статистических гипотез).
Основные задачи математической статистики делятся на параметрические и непараметрические. Если известны вид распределения и область изменения параметров и необходимо оценить их значения, это параметрическая задача. Если нет представления даже о законе распределения, не говоря уже о значениях параметров, задача является непараметрической.
Основные понятия выборочного метода
Результат n последовательных и независимых наблюдений над случайной величиной X, представляющей генеральную совокупность, рассматривается как случайная выборка. Конкретный набор выборочных значений x1,x2,…,xn следует рассматривать как одну из многих реализаций многомерной случайной величины X1,X2,…,Xn, компоненты которой независимы и имеют одну и ту же функцию распределения F(x), соответствующую генеральной совокупности:
F(x1,x2,…,xn) = P(X1<x1, X2<x2,…,Xn<xn) = 
Все выводы выборочного метода при изучении генеральной совокупности опираются только на выборочные значения и, возможно, некоторые априорные предположения о генеральной совокупности. Затем проверяется достоверность этих выводов по отношению ко всему возможному набору выборок, подчиняющихся распределению этой многомерной случайной величины.
Теоретическим законам распределения случайных величин и их числовым характеристикам в математической статистике ставятся в соответствие их статистические аналоги. Ряду распределения дискретной случайной величины соответствует вариационный ряд, который образуют записанные в возрастающем порядке наблюдаемые значения случайной величины (варианты) xi. Вероятности каждого значения случайной величины соответствует относительная частота каждой варианты, равная отношению частоты, т.е. количества наблюдений варианты ni, к общему числу наблюдений, т.е. объему выборки n = 
.
|
|
|
Статистическим распределением называется соответствие между вариантами и их частотами или относительными частотами. Многоугольнику распределения (ломаной, соединяющей точки с координатами (xi,pi)) соответствует полигон частот или относительных частот (ломаная, соединяющая точки (xi,ni) или точки (xi,nxi)). Модой называют варианту, имеющую наибольшую частоту. Медиана – это варианта, которая делит вариационный ряд на две части, равные по числу вариант.
Для непрерывных случайных величин вариационный ряд содержит интервалы значений (вариант) и суммы частот вариант, попавших в этот интервал, или их относительных частот. Статистическое распределение связывает интервалы вариант и соответствующие частоты попавших в них значений.
Теоретической функции распределения соответствует эмпирическая функция распределения. Функция распределения выборки F*(x) определяет для каждого значения x относительную частоту события X< x:
F*(x) = nx / n,
где nx – число вариант, меньших x; n – объем выборки. Из теоремы Бернулли следует, что
lim P [ │F(x) – F*(x)│< ε] = 1
n → ∞
Эмпирическая функция распределения служит для оценки теоретической функции распределения генеральной совокупности.
Законы распределения непрерывных случайных величин.
Нормальное распределение
Функция распределения F(x) определяет вероятность того, что случайная величина X в результате испытания примет значение, меньшее x:
F(x) = P(X < x).
Случайная величина называется непрерывной, если ее функция распределения F(x) есть непрерывная функция, кусочно-дифференцируемая с непрерывной производной.
Свойства F(x):
· значения F(x) удовлетворяют двустороннему неравенству 0 ≤ F(x) ≤ 1;
· F(x) – функция неубывающая;
· P(a ≤ X ≤ b) = F(b) – F(a).
Следствие. Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна 0.
Однако имеет смысл учитывать вероятность попадания значения случайной величины в определенный интервал, каким бы малым он ни был, что и определяется третьим свойством.
Непрерывную случайную величину можно задать с помощью плотности распределения. Плотность распределения вероятностей непрерывной случайной величины X называется функция f(x) = F'(x). Вероятность попадания значения случайной величины в заданный интервал вычисляется так:
P(a ≤ X ≤b) = 
График плотности распределения называется кривой распределения.
Свойства f(x): f(x) ≥ 0; 
=1. Это означает, что график расположен выше оси Ox, а площадь криволинейной трапеции, ограниченной кривой распределения, равна 1.
Кривой распределения генеральной совокупности непрерывных случайных величин соответствует гистограмма. Гистограмма частот – это ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению ni/h. Для гистограммы относительных частот высоты прямоугольников равны отношению nxi/h. Причем площадь гистограммы равна 1, как и площадь, ограниченная теоретической кривой распределения.
|
|
|
Числовые характеристики непрерывных случайных величин, заданных плотностью распределения f(x), вычисляются так:
математическое ожидание M(x) = 
;
дисперсия D(x) = 
;
среднее квадратическое отклонение σ(x) = 
.
При решении практических задач сталкиваются с различными распределениями непрерывной случайной величины. Плотности их распределения называются законами распределения. Часто встречаются законы: равномерной плотности, нормальный, показательный. Особую роль играет нормальный закон.
Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью:
Нормальное распределение определяется двумя параметрами: математическим ожиданием a и средним квадратическим отклонением σ. Графикплотности нормального распределения называется нормальной кривой или кривой Гаусса.
Свойства кривой распределения:
· При x=a функция имеет max = 1/ 
;
· Изменение величины параметра a не изменяет формы нормальной кривой, а только приводит к сдвигу вдоль оси Ox;
· С возрастанием σ максимальная ордината уменьшается, а сама кривая становится более пологой, а при убывании σ кривая становится более «остро вершинной»;
· Вероятность попадания нормальной случайной величины в заданный интервал
P(α < X < β) = Φ(
) - Φ 
,
где Φ(x) – функция Лапласа (табулированная функция, которая определяет вероятность попадания случайной величины в интервал (0,x)).
На рисунке приведена кривая распределения случайной величины, имеющей математическое ожидание a = 1 и σ = 2.
Абсолютная величина отклонения нормально распределенной случайной величины от математического ожидания не превосходит утроенного среднего квадратического отклонения. Это свойство называется «правилом 3σ». Если случайная величина обладает этим свойством, то есть основания предполагать, что она распределена нормально.
Нормально распределенные случайные величины широко распространены на практике. Это объясняется центральной предельной теоремой Ляпунова А.М.: если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному. Примером может служить суммарная ошибка измерений или вычислений.
При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это отличие. С этой целью вводят специальные характеристики, в частности асимметрию и эксцесс. Для нормального распределения они равны 0. Небольшие их значения дают возможность предположить, что распределение близко к нормальному.
Асимметрия теоретического распределения As = μ3/σ3, где μ3 - центральный момент 3-го порядка, σ – среднее квадратическое отклонение.
As > 0, если «длинная часть» кривой расположена справа от математического ожидания, и As < 0, если – слева.
Эксцесс теоретического распределения Ek = (μ4/σ4) – 3, где μ4 – центральный момент 4-го порядка. Для нормально распределенной случайной величины μ4/σ4 = 3 и Ek = 0. Если Ek > 0, кривая распределения имеет более высокую и острую вершину по сравнению с нормальной кривой, если Ek < 0 – более низкую и плоскую.
Кривая нормального распределения является очень важным понятием в статистике. Она является центральной для теории статистических исследований. В сочетании со стандартным отклонением она может быть использована и для построения точных описательных статистик эмпирического распределения.
Кривая нормального распределения – это теоретическая модель, представляющая собой абсолютно симметричный и гладкий вид полигона частот. Важнейшее свойство кривой нормального распределения – расстояние по абсциссе, измеренное в единицах стандартного отклонения s от среднего арифметического распределения, всегда дает одинаковую площадь под кривой. Эта площадь составляет 68,26% общей площади на отрезке [-s, s ]; 95,44% - на отрезке [-2s,2s ] и 99,72% – на отрезке [-3s,3s ]. В связи с этим имеет смысл рассматривать стандартизированные значения, т.е. выраженные в единицах стандартного отклонения: Z = (xi –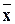 
)/s. Стандартизированная теоретическая кривая нормального распределения имеет среднее значение, равное 0, и стандартное отклонение, равное 1. Теоретическая кривая нормального распределения глубоко проанализирована и описана. Области, относящиеся ко всем Z-значениям, представлены в табличной форме (в таблице нормального распределения).
|
|
|
