Оценка параметров распределения.

Для оценки параметров распределения имеется два способа: точечный и интервальный. Точечные методы указывают лишь точку, около которой находится неизвестный оцениваемый параметр. С помощью интервальных способов можно найти интервал, который с достаточно большой вероятностью содержит неизвестное значение параметра.

Если известен закон распределения изучаемого признака генеральной совокупности, необходимо оценить параметры этого распределения. Оценка числового параметра θ является функцией выборочных значений и меняется от выборки к выборке

θ^* (X₁,X₂,…,X_n) = θ_n^* .

В определенном статистическом смысле она близка к истинному значению этого параметра. Статистическая оценка θ^* неизвестного параметра распределения θ должна удовлетворять следующим требованиям:

– должна быть несмещенной, т.е., что математическое ожидание θ^* должно быть равно оцениваемому параметру θ: M(θ^*) = θ, что означает отсутствие систематических ошибок;

– должна быть эффективной, при которой рассеяние возможных значений θ относительно M(θ^*) , т.е. дисперсия D(θ^*) – наименьшая;

– при больших объемах выборки должна быть состоятельной, т.е. должна при n → ∞ стремиться по вероятности к оцениваемому параметру:

P{│ θ^*– θ│≤ε} → 1 при n → ∞

Выборочные числовые характеристики служат точечными оценками числовых характеристик генеральной совокупности. Выборочное среднее

/ n,

вычисленное как среднее арифметическое выборочных значений, является несмещенной, состоятельной и эффективной точечной оценкой математического ожидания генеральной совокупности MX=m_x. Выборочная дисперсия, вычисленная как средняя взвешенная квадратов отклонений от выборочной средней,

D_в = 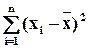/ n

является смещенной оценкой дисперсии генеральной совокупности. Исправленная выборочная дисперсия

S² = / (n-1) –

несмещенная точечная оценка дисперсии D_x. Оценками среднего квадратического отклонения генеральной совокупности являются: – смещенная и S –несмещенная, вычисленные по данным выборки. В случае большого объема выборки в качестве x_i берут представителей (обычно средины) интервалов, на которые разбивается весь диапазон значений исследуемого признака. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра.

Интервальная оценка определяется двумя числами – концами интервала. Они позволяют установить точность и надежность оценок.

Надежностью (доверительной вероятностью) оценки параметра θ по θ^* называется вероятность γ, с которойвыполняется неравенство │ θ - θ ^*│< δ:

P { │ θ - θ ^*│< δ } = γ

В качестве γ берут число, близкое к 1: 0,95; 0,99;0,999. Другими словами, надежность γ определяет вероятность того, что интервал (θ^* – δ; θ^* + δ) содержит θ. Интервал (θ^* – δ; θ^* + δ) называется доверительным.

Интервал (θ^* – δ; θ^* + δ) называется доверительным интервалом надежности 1- α для неизвестного параметра θ, если вероятность тех X, для которых выполнено неравенство θ^* – δ < θ < θ^* + δ, равна 1- α (α = 0,05; 0,01; 0,001) для любого допустимого θ. Надежность можно увеличить, расширив интервал (за счет увеличения δ) или увеличив число наблюдений.

Пример. Для оценки математического ожидания a нормального распределения f(x) = exp(-(x-a)²/(2σ²))/ наилучшей несмещенной точечной оценкой является выборочное среднее . При известном параметре σ доверительный интервал находится с помощью функции Лапласа:

P(a – δ < 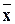< a + δ) = P ( 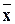– δ < a < 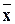+ δ) = 2Φ(δ /σ) = γ

Каково бы ни было a, интервал ( – δ; 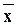+ δ ) накроетэтонеизвестное с вероятностью γ. Зная выборочное среднее, можно определить границы интервала.

При неизвестной дисперсии нормального распределения для оценки математического ожидания строят случайную величину

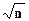T = ( – a) /s.

Разность – a – статистика, которая не зависит от начала отсчета. Она не будет зависеть и от масштаба, если ее разделить на оценку среднего квадратического отклонения выборочной средней s / . Этоделает ее нормальной случайной величиной с математическим ожиданием m_x = 0 и средним квадратическим отклонением σ = 1. Эта случайная величина имеет распределение Стьюдента с (n-1) степенями свободы. Критические границы распределения Стьюдента t_γ определяются условием: P { │t│< t_γ } = 1 – α = γ

Доверительный интервал для неизвестного параметра a при неизвестной дисперсии σ²: ( – t_γs/ ; + t_γs/ ). Значения t_γ (γ; n) находят из таблицы распределения Стьюдента по значениям надежности γ и объему выборки n. При неограниченном возрастании объема выборки распределение Стьюдента стремится к нормальному распределению (n > 30). Для малых выборок (n < 30) замена распределения нормальным приводит к грубым ошибкам, а именно к неоправданному сужению доверительного интервала, т.е. к повышению точности оценки. Так при n = 5 и γ = 0,99t_γ = 4,6 по статистике T, а по функции Лапласа t_γ = δ / σ = 2,58.

Кроме выборочных средней и дисперсии применяются оценки и других числовых характеристик по характеристикам вариационного ряда. Оценки асимметрии и эксцесса выражаются через выборочные центральные моменты 3-го и 4-го порядка и выборочное среднее квадратическое отклонение.