 |
Пространственные группы симметрии Федорова
|
|
|
|
Законы симметрии распространяются не только на внешнюю форму кристаллов, но и на их внутренне атомное строение. В 1890 г. Е.С. Федоров вывел строго математическим путем все возможные сочетания элементов симметрии в пространстве. Он доказал, что таких пространственных групп симметрии может 230. Этот вывод стал основой современной кристаллохимии – теорией атомной структуры кристаллов.
Изучение внутренней структуры кристалла значительно сложнее изучения внешней симметрии, так как увеличивается разнообразие элементов симметрии и имеется бесконечное число тождественных элементов симметрии: параллельно каждой оси или плоскости симметрии имеется бесконечное количество осей и плоскостей симметрии, а соответственно, и центров симметрии.
Принцип вывода пространственных групп симметрии изложен в следующих учебниках:
Г.Б. Бокий. Кристаллохимия. – М.: Наука, 1971. – 400 с.
В.С. Урусов. Теоретическая кристаллохимия. – М.: Изд-во МГУ, 1987. – 275 с.
Ю.Г. Егоров-Тисменко. Кристаллография и кристаллохимия. – М.: КДУ, 2005. – 592 с
Координационные числа, координационные полиэдры, число формульных единиц
Для описания атомного строения кристалла в кристаллохимии прибегают к приему разбиения полной картины на отдельные фрагменты. При таком разбиении структуры придается значение ближайшему координационному окружению каждой из частиц, что позволяет однозначно описать индивидуальные особенности каждой кристаллической структуры. Этот подход называется стехиометрическим и использует три основные понятия: координационное число (КЧ), координационный полиэдр (КП) и число формульных единиц (Z).
Координационным числом (КЧ) называется число ближайших соседей некоторого данного атома в структуре кристалла. Если речь идет о КЧ иона, то имеется в виду число ближайших ионов другого знака.
|
|
|
Пример.
Координационное число
В ионном кристалле хлорида натрия каждый ион хлора окружен шестью ионами натрия и наоборот, следовательно, КЧNa/Cl = 6 и КЧCl/Na = 6.
В структуре флюорита (ионный кристалл CaF2) каждый ион кальция окружен восьмью ионами фтора, а каждый ион фтора четырьмя ионами кальция, следовательно, КЧСа/F = 8, КЧF/Ca = 4.
Координационный полиэдр (КП) получается, если соединить прямыми линиями центры атомов, составляющих ближайшее окружение данного атома. Построение КП позволяет охарактеризовать геометрию расположения частиц вокруг центрального атома.
Число теоретически возможных КП растет с увеличением количества вершин: тетраэдр возможен только один, пятивершинников может быть 2 – тригональная бипирамида и тетрагональная пирамида, шестивершинников – 7, семивершинников – 34 и т. д. Большинство не реализуется в кристаллических структурах.
Притупленный октаэдр Пентагондодекаэдр Ромбододекаэдр
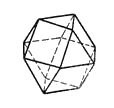
| Икосаэдр | Притупленный тетраэдр | Кубооктаэдр | Кубооктаэдр |
| 
| 
| 
|
Трехшапочная тригональная призма
| Куб | Квадратная антипризма | Тригональный додекаэдр | Двухшапочная призма |
| 
| 
| 
|
| Одношапочная тригональная призма | Семивершинник |
| 
|
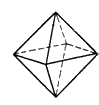
| Октаэдр | Тригональная призма |
| 
|
| Тетрагональная пирамида | Тригональная бипирамида |
| 
|
| Тетраэдр | Квадрат |
| 
|
Треугольник
В реальных кристаллических структурах реализуются КЧ 24 (КП – притупленный октаэдр), 20 (КП – пентагондодекаэдр), 14 (КП – ромбододекаэдр), 12 (КП – икосаэдр, притупленный тетраэдр, кубооктаэдр, гексагональный кубооктаэдр), 9 (КП – трехшапочная тригональная призма), 8 (КП – куб, квадратная антипризма, тригональный додекаэдр, двухшапочная призма), 7 (КП – одношапочная тригональная призма, семивершинник), 6 (КП – октаэдр, тригональная призма), 5 (КП – тетрагональная пирамида, тригональная бипирамида), 4 (КП – тетраэдр, квадрат), 3 (КП – треугольник), 2 (КП – уголок), 1 (КП – гантель) и др.
|
|
|
Чаще всего встречаются в кристаллах КП, которые имеют только треугольные и четырехугольные грани. Однако для структур интерметаллидов известны КП с шести- и восьмиугольными гранями. Если расстояние от центра КП до его вершин равны, то он может быть вписан в сферу. Поэтому для обозначения ближайшего окружения часто используют термин координационная сфера.
Правильные КП встречаются обычно в кристаллических структурах простых и бинарных соединений с высокой симметрией. Для сложных соединений с низкосимметричными структурами более характерны искаженные КП с различной степенью искажения, которое вызывается конкретными условиями взаимной упаковки разных атомных комплексов в кристалле. Согласно модели заряженных сфер отталкивание между лигандами определяет форму КП, если существует выбор между различными КП при одном и том же КЧ. Размещение лигандов на координационной сфере определяется условием минимума энергии отталкивания лигандов.
Число формульных единиц (Z) соответствует числу атомов приходящихся на одну элементарную ячейку. Для простых веществ, состоящих из атомов одного элемента (Cu, Al и др.) число формульных единиц равно числу атомов в ячейке Бравэ. Для простых молекулярных веществ (I2 и др.) и молекулярных кристаллов (H2O и др.) число формульных единиц равно числу молекул в элементарной ячейке. В ионных кристаллах (NaCl и др.) и интерметаллидах (CuAu и др.) рассчитывается суммарное число формульных единиц на одну элементарную ячейку.
Число формульных единиц определяется экспериментально при рентгеновском исследовании вещества. В первую очередь вычисляются параметры элементарной ячейки и её объем, затем рассчитывается число формульных единиц:
где V – объем элементарной ячейки, A3; r - плотность, г/см3; М – молекулярная масса вещества; 1,64?10-24 – масса атома водорода, г.
Атомно-кристаллическая структура - конкретное распределение материальных частиц (атомов, ионов, групп атомов и т.д.) в пространстве. Понятие структуры непосредственно связано с такими понятиями как правильная система точек, кратность, значность, число степеней свободы, межатомные расстояния и валентные углы.
|
|
|
Правильной системой точек называется совокупность симметрично- эквивалентных позиций (точек), связанных между собой операциями симметрии пространственной группы. Правильную систему точек можно получить из одной точки, повторив ее при помощи всех операций симметрии, свойственных данной пространственной группе. Правильная система точек характеризует геометрические законы пространственного расположения материальных частиц в кристалле. Для правильной системы точек существуют понятие общей и частной систем. Частная правильная система точек образуется, если исходная точка лежит хотя бы на одном из элементов симметрии или отстоит на равных расстояниях от одинаковых элементов симметрии. Общая правильная система точек получается, если исходная точка (а значит, и все остальные, ей симметрично эквивалентные) не соприкасается ни с одним из элементов симметрии и лежит не на равных расстояниях от одинаковых элементов симметрии.
Кратностью правильной системы точек называется число точек каждой правильной системы, приходящихся на объем элементарной ячейки. У точек общей правильной системы кратность выше, чем у частной.
Формульная единица - стехиометрический состав вещества, описываемый химической формулой. Для молекулярных кристаллов понятие "формульная единица" совпадает с понятием "молекула". Число формульных единиц в ячейке (z) - количество атомов простого вещества или число "молекул" соединений, приходящееся на элементарную ячейку. Например, для P- ячейки: z= 8 (атомов в вершинах ячейки) x 1/8=1; для -I -ячейки: z=8 (атомов в вершинах ячейки) x 1/8+1 (атом в центре ячейки) =2; для F-ячейки: z=8 (атомов в вершинах ячейки) x 1/8 + 6 (атомов в центрах грани) x 1/2 =4; для С- ячейки: 8 (атомов в вершинах ячейки) x 1/8+2 (атома в центрах двух параллельных граней) x 1/2=2.
Каждая точка, находящаяся на элементе симметрии, имеет определенную значность, показывающую, из слияния скольких точек общего положения получилась точка частного положения. Значность характеризует симметрию положения: чем выше значность, тем выше симметрия данной позиции. Произведение значности точки на ее кратность есть величина постоянная для данной пространственной группы, равная кратности точки общего положения.
|
|
|
Положение точки (материальной частицы: атома, иона, молекулы и т д.) описывается при помощи трех координат, которые характеризуют степень свободы точек. Точка, занимающая любое положение внутри элементарной ячейки, имеет 3 степени свободы; точка, расположенная на плоскости, - 2 степени свободы; точка, находящаяся на осях симметрии, имеет 1 степень свободы. Если точка, например, располагается в точке пересечения оси с плоскостью симметрии, то число степеней свободы у такой точки равняется нулю.
|
|
|
