 |
Понятие математического моделирования в ТЭС и установках
|
|
|
|
Понятие математического моделирования в ТЭС и установках
Выделяют физическое и математическое моделирование. При физическом моделировании изучение процесса или явления происходит при его воспроизведении в различных масштабах и анализе влияния физических особенностей и линейных размеров.
При физическом моделировании эксперимент проводится на изучаемом физическом процессе, а результаты эксперимента представлены в форме зависимостей безразмерных комплексов.
Эти комплексы распространяют эксперимент и установленные зависимости на группу подобных явлений и называю критериями подобия.
Физическое моделирование требует большого капиталовложения и затрат времени для эксперимента. Оно целесообразно в случае если нет возможности математического моделирования или задача сложна для математического моделирования.
При математическом моделировании изучены параметры реального объекта, которые имею математическое описание и связаны математическими отношениями в аналитических зависимостях(уравнениях), описывающих моделируемый объект.
Математическая модель реального объекта- абстрактный математический объект поставлены в соответствующий реальному физическому процессу, явлению или объекту и под математической модели объекта понимается совокупность соотношений, которые связывают некоторую переменную, информацию относящуюся к моделируемому объекту с исходной информацией и данными.
При математическом моделировании выделяют этапы:
1. Постановка задачи изучение свойств и особенностей рабочей модели объекта определяющей исходные параметры, формулируется цель исследования моделирование и целевые функции;
|
|
|
2. Разработка математической модели дается описание моделируемых процессов и объектов в виде математической зависимости при этом учитываются геометрический и термодинамические параметры исследуемый объект в этом этапе разрабатывается алгоритм выбираются числа методы решения постановки задачи и реализуется алгоритм на языке программирования;
3. Проведение исследования выполняются расчеты и оценивается правильность работы данного алгоритма;
4. Переназначение, полученных при математическом моделировании на реальный объект изучения получает результат подлежащее экспериментальной проверки для установления реальности модели;
Выделяют статические и динамические модели.

 -исходные геометрические термодинамические параметры;
-исходные геометрические термодинамические параметры;
y-вектор зависимых переменных от исходных данных.
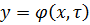

Имеем дело c статической моделью.

Имеем дело с динамической моделью.
Графо - аналитическое моделирование
При графо- аналитическом моделировании системы виде графов, а ее решение с использованием различных видов матриц составляющих на основании информации заключенной в графе.
Граф представляет собой совокупность отрезков или векторов в произвольной длины и формы, соединяющих между собой точки, являющейся вершинами графа и отражающие элементы моделируемой системы (отрезки, ребра, вектора-дуги).
Отрезки и дуги показывает связь между элементами, вершинами графа по определённым видам энергоносителей.
Рассмотрим в качестве примера воровство газотурбинной установки.
| |
 |


 |
I. Пароперегреватель;
II. Турбины высокого давления;
III. Паровой котел;
IV. Электрогенератор;
V. Турбины низкого давления;
VI. Конденсатор;
VII. Подогреватель;
|
|
|
VIII. Устройство производящее отвод пара;
IX. Насос.
Носители:
1-воздух
2-топливо
3-продукты сгорания
4-перегретый пар
5-механическая энергия
6-электрическая энергия
7-влажный пар
8-вода

На основании графа строится структурной матрицы вида:
- связи
- соединение
Матрица связей количество строк количество связей (дуг) в графе количество столбцов количество энергоносителей. Она состоит из нулей и единиц.
Элемент матрицы 0, если в i-ой связи отсутствует j-ой энергоноситель.
1, если в i-ой связи присутствуют j-ой энергоноситель.
Матрица соединений.
Строки номера связей в графе, а столбцы номера элементов принципиальной схеме, состоит из 0, 1 и -1.
0, если i-ая связь не связанны с j-ым элементом;
-1, если i-ая связь входит в j-ый элемент;
1, если i-ая связь выходит из j-ого элемента;
| I | II | III | IV | V | VI | VII | VIII | IX | |
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 | |||||||||
| -1 |
Матрица связей и соединений являются структурными матрицами, так как дают однозначное описание всех потоков энергоносителей между отдельными структурными электросистемами и позволяют перевести на язык матричной алгебры, что имеет важное значение при математическом моделировании.
|
|
|
|
|
|


