 |
Методика построения потоковых графов.
|
|
|
|
Методика построения потоковых графов.
1. Изучается физико-химическая сущность тепловых процессов в элементах системы и строится её принципиальная схема, при этом отключаются все входящие и выходящие потоки.
2. Определяются все виды энергоносителей в данной схеме и все их истоки и стоки.
3. Отображается графически потоковый граф, при этом избегаю пересечения дуг. Отмечаются все элементы и все источники, истоки для всех видов энергоносителей. Все источники истоки номеруются по номеру потока исходящего или подходящего к ним.
Рассмотрим пример построения для химического реактора:
A+B=> E+∆ U
На теплообменник подводится Aи B в II химическом реакторе происходит экзотермическая реакция с образованием Е и энергии. Затем компонента Е выводится, а компонента А проходит через теплообменник => охлаждение смеси => охлажденная А подается на I теплообменник смешивания.
L1=A+B (компонент)
L2=A+B (смесь)
L3=A+E (смесь)
L4=E
L5=A
L6, L7 поток охлаждения до теплообменника охлаждения L8 поток охлажденной компоненты А.
|
|
 | |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
|
| ||||||||||
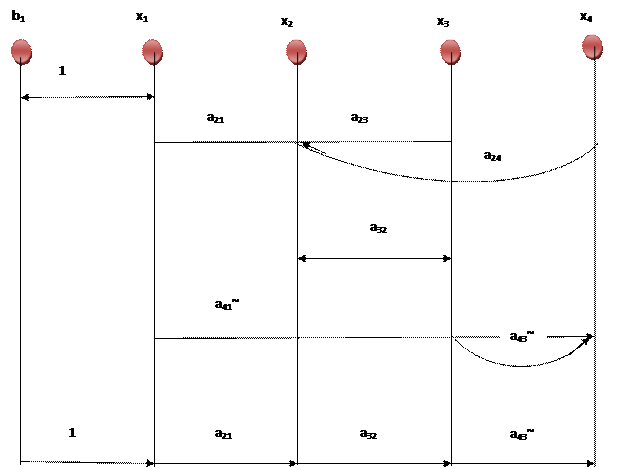
Материальные потоковые графы строятся исходя из параметрического графа и в нем отмечаются все элементы, в которых массовое изменение соответствующей компоненты, а так же отмечаются все реальные и мнимые стоки и истоки данной компоненты и все связанные с ними элементы.
 | |||||||||||
| |||||||||||
|
| ||||||||||
| |||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общий материальный потоковый граф отображает изменение элементов, в которых происходят массовые изменения всей газовой смеси.
(4)
Суть метода состоит в том, что данная матрица заменяется на 3 линейных массива.
Все три элемента находятся на диагонали матрицы.
Система:
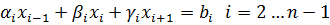(5)
Решение системы (5) даётся в виде рекуррентной формулы.
(6)
i=1…n-1
Чтобы найти 
определяют 
и 
. Для нахождения используем понятие индекса в формуле (6).
=> 
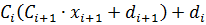(7)
Выполним алгебраическое преобразование:
(8)
(9)
Решение системы уравнений методом прогонки в 2 этапа:
1. Прямой ход по рекуррентным формулам (9) определяем 
и ;
2. Обратный ход по рекуррентной формуле (6) определяем значение . Для осуществления решения необходимо определить стартовые значения коэффициентов C и d.
При i=1 из (9)
Из формулы (6) выражаем значения для 
(i=n-1).
Пример:
Система:
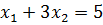
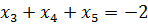
Заданы значения:
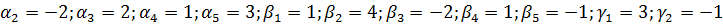
По рекуррентным формулам находим:
С2=-3; С3=0, 1; С4=-0, 5; С5=-2, 2502; d2=5; d3=1. 1; d4=-0. 4; d5=-3. 5004;
По формуле находим переменные:
Таким образом:
x1=0. 084; x2=1. 1; x3=3. 23; x4=-7. 26; x5=-1. 67
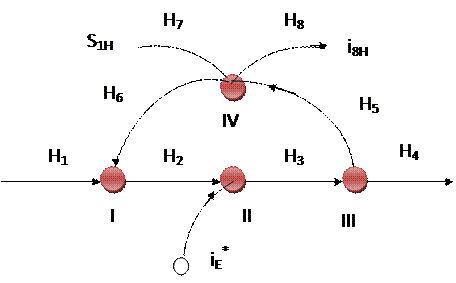
тепловой потоковый граф строится на основании параметрического графа. В нем отмечаются реальные и мнимые стоки и истоки тепла.
 | |||||
| |||||
| |||||
Информационные графы.
Вершинами информационного графа являются уравнения модели системы или установки, а также источники информации.
Ветви- информационные потоки соответствующие информационным переменным системы уравнений. Информационные графы для системы уравнений могут быть циклическими и ациклическими. Также они отображают стратегию решения данной системы уравнений. Циклический граф содержит хотя бы один контур и для его осуществления потребуется воспроизведение итерационного процесса.
|
|
|
Сигнальные графы.
Взвешенные графы соответствуют линейной системе уравнений математического моделирования и отражают причинно-следственные и информационно-параметрические свойства между информационными переменными системы уравнений.
Вершины сигнального графа- это информационные переменные, а каждая ветвь связь между переменными, каждая связь имеет все = коэффициенту регистрирующему связь между сигналами. Вершина истока отображает связь информационных переменных. Вершина стока отображает зависимые переменные, т. е. результат. Например, ветви указанные от вершины- сигнал, а указанные к вершине отображение сигнала, т. е. следствие.
При построении сигнального графа по исходной системе линейных уравнений используются правила: сигналы передаются вдоль ветвей в направлении их ориентации, сигнал, проходящий вдоль ветви * коэффициент передачи этой ветви.
Сигнал, изображенный какой-либо зависимой вершиной, является алгебраической суммой сигналов поступающих в вершину по ветви. Величина сигнала изображенного зависимой вершиной передается по всем ветвям, выходящим из данной вершины.
Система:
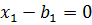
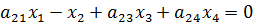
В качестве вершин графа используются переменные 
.
Система:
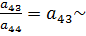
Решение сигнального графа процедура определения эквивалентных коэффициенту передачи между любой вершиной и стоком либо между зависимыми вершинами. Для ускорения процедуры решения системы с помощью любого вида графов целесообразно использовать эквивалентные преобразования.
1) Передача последовательных ветвей равно произведению передач этих ветвей.
|
|
|
|
|
 | |||||||
|
| ||||||
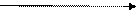
x2=ax1; x3=bx2; => x3=abx1
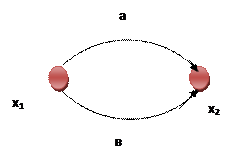
2) Передача параллельных ветвей равна сумме передач этих ветвей.
|
|
|
 | |||
 | |||
3) Устранение простой вершины, которая не входит в контур или петлю.
 | |||
 | |||
X4=ax1
X2=bx4
X3=cx4
X2=abx1
X3=bcx1
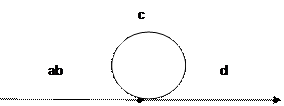
4) Исключение петли
 | ||||||||||||||||||||
|
|
| ||||||||||||||||||
 |  | |||||||||||||||||||
|
|
| ||||||||||||||||||
X2=(a/1-T)x1
X3=bx2
X2=ax1+Tx2
 | ||||||||||||||||||||||
|
|
| ||||||||||||||||||||
 | ||||||||||||||||||||||
 |  | |||||||||||||||||||||
|
|
| ||||||||||||||||||||
|
 | |||||||||
| |||||||||
| |||||||||
 | |||||||||
| |||||||||
|
|
|
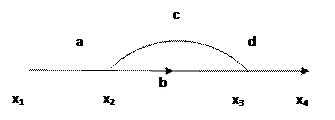
1) Необходимо изменить направление все ветвей прямого пути или контура на противоположное;
2) Изменить передачи на обратные от первого истока к новому истоку;
3) Переместить конец ветви, касающейся инвертированного измененного пути в новую вершину, в которую переносится инвертированная ветвь, оставив начало этой ветви в старой вершине;
4) Коэффициент передачи инвертированного пути является обратной величиной коэффициента передачи исходного прямого пути;
|
|
|
