Аппроксимация функции с помощью интерполяционных многочленов.

Аппроксимация функции с помощью интерполяционных многочленов.

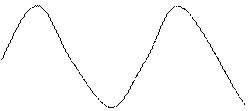
Замена одной функции другой называется аппроксимацией функции. Основание может быть табличным способом её задания.

A=x₀< x₁< x₂< …< x_i< …< x_n=b

X_i=> y_i

 

x	X0	X1	…	xi	…	xn
F(x)	Y0	Y1	…	yi	…	yn

 

Y=F(x)

Если x и y существует функциональная зависимость можно поставить задачу о представлении аналитических функций F(x).

X₀, x_n- узлы функции и если расстояние между узлами h=x_i-x_i-1=const, то сетка равномерная.

Классический подход к решению заключается в том, чтобы подобрать функцию G(x)  в некотором смысле подобную F(x), тогда F(x) аппроксимируемая функция, а F(G) – аппроксимирующая функция. Задача аппроксимации решается с использованием многочленов. Если аппроксимирующая функция совпадает в узлах сетки, то аппроксимирование называется интерполированием, а узлы сетки узлами интерполяции.

 

 

 

 

 

                                                               F(x)                               

 

 

                                                       G(x)  

 

Построение интерполяционного многочлена Лагранжа.

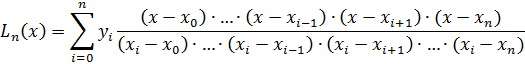
	X0	X1	X2
x
F(x)

 

      F(x)

 

                                                                                                  x

            1  3   4

 

 

 

Функция Ньютона даёт формулу итерационного многочлена Лагранжа записанного с использованием конечных разностей функции. Для функции заданной таблично с постоянным шагом линии.

Разность между значениями в соседних узлах сетки, называют конечной разностью 1 рода.

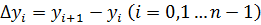
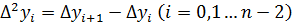
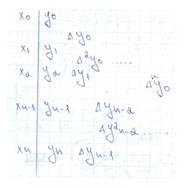
После него найдены пограничные коэффициенты рассчитывается температурное поле по следующим функциям:

T_i= 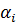 T_i+1+ 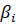 , где i=n-1…1

В качестве исходного значения необходимо определить температуру на правой границе и совершить это с граничным условием 2 рода.

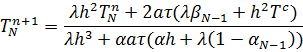
Задача

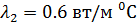Рассчитать температурное поле в составном стержне через три минуты длина стержня L=0. 09 м, t₀=20 ⁰C, , . Для второй части стержня, , . Для третьей части стержня, , 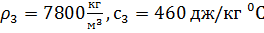. На левой границе х=0  t=-20⁰C. На правой границе x=l параметры части будем считать равными по 0, 03 при построении сетки в 1 части 2 отрезка разбиения n₁=2 во второй n₂=4 и в третьей n₃=3.

N=n₁+n₂+n₃+1=10

 

Моделирование распределения тепловых и электрических нагрузок на ТЭЦ.

Принцип распределения нагрузок между конденсационными энергоблоками. При одновременной работе нескольких энергоблоков возможна задача определения нагрева каждого. Цель распределения достижение максимума экономии топлива в энергосистеме.

Рассмотрим задачу распределения активной мощности системы при сохранении постоянной отдачи потребителям. Критерием оптимизации является минимизация расхода топлива, а в условиях применения различного топлива, критерием является минимизация затрат на топливо. Агрегаты, расположенные в пределах одной станции при условиях постоянства отпуска энергии потребителю можно заменить постоянством отпуска энергии в сеть.

N_ст=N₁+N₂+…+N_n= ,

Где N_ст- мощность генерируемая станцией и отпускаемая в сеть;

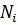- мощность, отдаваемая в сеть i-ым энергоблоком;

Суммарная нормативная мощность больше чем мощность, отдаваемая в сеть. Энергоблоки работают с недогрузкой. Суммарный расход всеми энергоблоками:

В_ст=В₁+В₂+…+В_n=

- Количество блоков;

В этом случае суммарные затраты на топливо:

В₁Ц_Т1+В₂Ц_Т2+…+В_nЦ_Тn=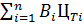

Для определения минимума расхода топлива на станции, которая является функцией многих переменных, ограниченных уравнением связи будет использовать метод неопределенных множителей Лагранжа.

Функция Лагранжа запишется:

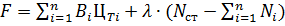                                                 (1)

Очевидно, что условия наиболее выгодного распределения нагрузок определяется из решения систем уравнения.

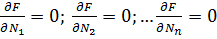                                                                (2)

С учётом выражения (1) условие записывается следующим образом:

                                                                      (3)

В данном случае - относительный прирост расхода топлива на i-ом энергоблоке при рассматриваемом решении работы.

При одинаковой стоимости топлива для всех энергоблоков условие (3) запишется без учета  .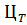

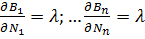- условие выгодного распределения нагрузки;

Условие самого выгодного распределения нагрузки между отдельными блоками может быть достигнуто за счёт большей загрузки блоков имеющих не высокий относительный расход и меньшей разгрузки блоков имеющих высокое значение расходов топлива. Продолжать до тех пор пока относительный расход не примет равное значение.

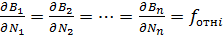                                                                 (3/)

Решение задач относительного распределения нагрузки можно провести на примере когда число энергоблоков =2.

При этом задаётся зависимость относительного прироста расхода топлива для мощности из каждого энергоблока.

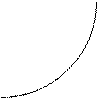
Затем проведя сечения линиями относительного прироста параллельно оси абсцисс исходя из заданного на 1- ом энергоблоке определяем мощность на 2- ом энергоблоке. Просуммировав мощности строим кривые зависимости оптимальной мощности для каждого блока.

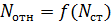
Исходя из этого определяем оптимальную мощность 1 и 2 блоков. При заданной мощности отдаваемой станцией в сеть.

               

		Nотн(N1/; N2/)

 

N1отн

N2 отн

N1+N2

                  

 

При решении оптимизации уравнения (3/) должны учитываться колебания удельных расходов топлива обусловленных изломами и скачками функции расхода топлива от генерирующей мощности станции. Также следует учитывать скачкообразные расходы, которые обусловлены изменением состава рабочего оборудования или изменения отдельных характеристик оборудования. Наличие условий в зависимости удельного расхода от нагрузки может быть открытие станков, что приводит к непрерывности зависимости расхода топлива.

В этом случае расход оптимального распределения нагрузок с помощью зависимостей относительных приростов расхода топлива сильно усложняется. Изменение нагрузки отдельных энергоблоков может производится до тех пор пока их мощность не достигнет предельных значений. N_min или N_max блок выводится из рассмотрения.

Другим способом решения задачи оптимального распределения нагрузки с учётом имеющихся ограничений является введение в расчёт штрафных функций. Суть этого метода заключается в том, что к основному уравнению Лагранжа добавляется дополнительный член, который при выходе за пределы ограничений даёт резкое увеличение функций расхода топлива.

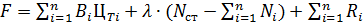                                    (4)

Величина 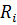 штрафной функции выбирается так, что она была аналитически простой и легко дифференцировалась. Чем больше значение будет принимать величина штрафной функции по мере выхода за пределы N_min и N_max тем больше вероятностей, что в процессе решения мы не выйдем за пределы установленных ограничений. Исходя из (4) запишем:

                                                                       (5)

Характерным примером может служить следующее представление:

R=a(N-N_max)       N> N_max

R=0 при N [ N_min; N_max]

R=a (N-N_min)  N< N_min

a- Произвольный коэффициент, определяющий угол наклона штрафной функции;

Решение задачи оптимального распределения нагрузок достигается приравниванием к нулю функции Лагранжа, которая задана уравнением
(2).

Зависимость функции Лагранжа от генерирующей мощности:

 

       R

 

                              N_min        N_max                                   N

 

          

            

 

                                                                                                         N

Из графика следует, штрафная функция не влияет на результаты расчёта внутренней зоны ограничений N_min - N_max, если решение выходит за пределы, то она не допускает выхода решения за пределы отмеченного диапазона. Оптимизация распределения нагрузок методом относительных приростов сложной задачей при большом количестве энергоблоков.

При нагрузок КЭС этот метод удобен и получил практическое распространение. Определение действительных значений относительных приростов учитывающих изменение эксплуатационных характеристик оборудования (температуры воды, уходящих газов).

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: