 |
Балансовые уравнения математической модели теплоэнергетической системы
|
|
|
|
Балансовые уравнения математической модели теплоэнергетической системы
Система уравнений балансов для элементов энергетического оборудования устанавливают соответствие между термодинамическими и расходными параметрами свойства которых обеспечивают получение заданной стационарной нагрузки, энергии установки с окружающими конструктивно-компоновочными характеристиками.
Зависимость между характеристиками связи можно описать уравнением баланса энергии расходного и гидравлического, а также уравнения изменения энтальпии для каждого из энергоносителей.
Уравнение баланса энергии:
- количество связей в системе;
l- порядковый номер энергоносителя;
-коэффициент учитывающий потери в окружающую среду:
G- расход энергоносителя;
H- энтальпия;
P- мощность;
N- количество генерирующих мощностей в системе.
Уравнения балансного расхода для l-ого энергоносителя в k- ом элементе.
Уравнение гидравлического (аэродинамического) баланса для l-ого энергоносителя в k- ом элементе.
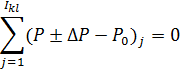
Уравнения изменения энтальпии l-ого энергоносителя в k- ом элементе.
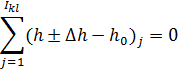
Например, для пароперегревателя необходимо 5 уравнений:
· Теплового баланса;
· Материального баланса расхода пара;
· Расхода продуктов сгорания;
· Уравнение гидравлического баланса напора пара;
· Уравнение аэродинамики баланса по продуктам сгорания.
Упражнения
Метод Гаусса
Система:
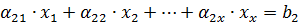
. (1)
.
.
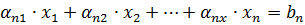
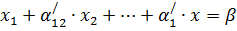(2)
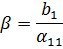
· Метод определителей Крамера;
· Матричный метод 
;
· Методы сводящиеся к исключению неизвестных (Гаусса);
|
|
|
Суть метода Гаусса сводится к тому, что матрица коэффициенты системы уравнений приводится к треугольному виду. Затем из системы уравнений последовательно находятся неизвестные.
Наиболее часто используется способ единичного деления. Исходно рассматривают первое уравнение системы коэффициент при переменной 
- ведущий коэффициент, выбирают и на него почленно делят все уравнения.
Последовательно умножаем уравнение (2) на коэффициент при на следующее уравнение системы и почленно вычитают друг из друга.
Система:
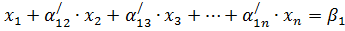
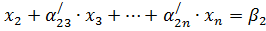
Задание:
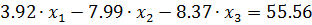
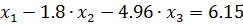
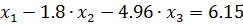
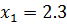
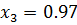
Описание характеристик оборудования
Для выполнения совместного теплового, гидравлического расчёта в установке необходимо установить зависимость между термодинамическими и техническими характеристиками элементов оборудования. В качестве таких характеристик можно принимать следующее:
· Характеристика изменения давления для каждого L-ого энергоносителя в К-ом элементе
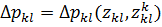(5)
- конструктивные особенности К-ого элемента оборудования;
-общая совокупность конструктивных параметров описывающих установку;
· Характеристика изменения температуры L-ого энергоносителя в К-ом элементе
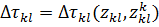(6)
· Характеристика изменения расхода каждого L-ого энергоносителя в К-ом элементе
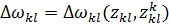(7)
· Характеристика средней скорости потока L-ого энергоносителя в К-ом элементе
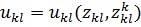(8)
· Характеристика максимальной температуры сжатия для каждой q-ой конструктивной части К-ого элемента из m-ого материала
(9)
|
|
|
· Характеристика сжатия q-ой конструктивной части К-ого элемента из m-ого материала
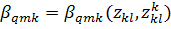(10)
· Характеристика расходов металла и других материалов для q-ого конструктивной части К-ого элемента из m-ого материала
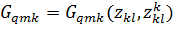(11)
Следующим шагом является установление ограничений:
Термодинамические расходные и конструктивные параметры не могут принимать произвольных значений, изменяться в пределах физически возможных и технически осуществимых, а так же в пределах технически допустимых качественных и эксплуатационных состояний в узлах конструктивных элементов (влажность пара в конце расширения ограниченно установленными эрозиями лопаток в последней турбине, давление пара в данном регенеративном отборе не должно быть выше, чем в предыдущем и ниже чем в последнем).
Таким образом, уравнения с 1-11 и система ограничений определяют в многомерном пространстве некоторую область допустимых параметров, в пределах которой осуществляется решение балансовых уравнений.
В качестве целевой функции осуществления моделирования может использоваться минимальное или максимальное значение какого-либо параметра оптимизируемого по различным вариантам расчёта.
Наиболее часто в качестве целевой функции используется минимизация затрат:
- номинальные издержки за год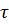 
;
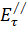- эксплуатационные издержки за год ;
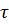- ежегодные издержки при нормальной эксплуатации 
;
- коэффициент приведения затрат.
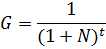
Непременным условием составление вариантов теплоэнергетические установки является приведение их к одинаковому энергетическому эффекту. Это требование означает необходимость выравнивания вариантов по полезному отпуску электрической и тепловой энергии в системе по всем генерирующим мощностям. Для варианта по обеспечению электрической энергии (выражение по потреблению энергии) целевая функция принимает вид:
Индекс S- замещаемая станция или агрегат;
R- режимные периоды в году;
R- общее число режимных периодов;
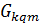- расход m-ого материала на q-ый элемент k-ого узла;
- коэффициент расхода m-ого материала учитывающий потери при изготовлении, транспортировки и монтаже;
|
|
|
- коэффициент потерь топлива;
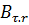- расход топлива в r-ом периоде за год ;
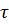- мощность, используемая для собственных нужд, генерируемая в период r года 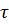за счёт l-ого энергоносителя;
- коэффициент, учитывающий потери по замещаемой станции или агрегату;
- длительность r-ого периода за год ;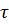
- приведенная стоимость или цена материала;
- удельные затраты на топлива за r-ый период года ;
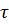- коэффициент отчисления за r-ый период года 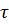на амортизацию, текущий ремонт, заработную плату и общие эксплуатационные расходы.
В качестве условия сопоставимости агрегатов используют:
1. Во всех вариантах расчётов применяется номинальные мощности электрических агрегатов равными;
2. Для обеспечение равенства мощностей электрической энергии в сеть для различных агрегатов и станций допускается возможность варьирования в заданных пределах мощности электрического генератора (5-10%);
Сопоставление вариантов осуществляется по критерию затрат. Таким образом, математическая модель теплоэнергетической системы совокупность балансовых уравнений (1-4), динамических характеристик (5-11) и совокупность ограничений, а также целевую функцию.
Можно выделить особенности построения математической модели отдельных узлов установок.
Дополнение к описанной модели включает:
- технические и технологические параметры характеризующие узел;
-подробные конструктивно компоновочные признаки узла;
-подробные характеристики применяемых материалов.
Как правило при оптимизации параметров узла производится оптимизации его параметров. При совместном рассмотрении группы узлов оптимизированные параметры расширяются и можно говорить об оптимизации термодинамических параметров.
Окончательное решение оптимизации узла принимается в результате комплексной оптимизации установки или система в целом так как существует тесная связь между отдельными элементами по потоком различных энергоносителей. При решении балансовых уравнений, которые имею нелинейный вид, используется метод Ньютона, метод простых итераций, градиентный метод.
|
|
|
Алгоритм расчёта теплоэнергетической установки:
 |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
Включает в себя три контура:
1- Независимый (11, 9)
2- вложенных (3, 4, 2... )
Разрывается обратной связи 58 14 и затем осуществляется расчёта элементов полей разрыва.
5, 8 рассчитывают элементы. 1-6 находит параметры потока 9. Затем прочитываются 7 и 8 элементы разрывается связь 14 и рассчитывают 9 10 11. Находим параметры потока 15. Затем рассчитывается 12 элемент и находим параметры потока 16. Правильным выбором разрывных потоков можно уменьшить размерность системы уравнений описывающих систему. Как правило бывают более выгодна с точки зрения скорости решать несколько систем уравнений меньшего порядка. Для системы более высокого порядка существует 2 приёма с помощью которых удается уменьшить размерность системы: выделение в системе совокупности элементов охватываемых обратными связями -обратными контурами и элементов не входящих в контуры, тогда расчёт системы сводится к решению систем уравнений контуров и отдельному решению уравнения, и системы описывающих отдельные элементы.
|
|
|
