 |
Упражнения. Продолжение лекций
|
|
|
|
Упражнения
Конечные разности любого порядка представленные через значения функции:
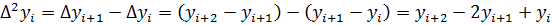
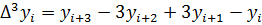
С учётом использования разностей может быть записан интерполяционный многочлен, аппроксимирующий функцию задано таблично:
Первая интерполяционная формула Ньютона. Кроме этого используется форма записи.
Кроме этого используется форма записи:
h- шаг сетки.
X=x0+ht
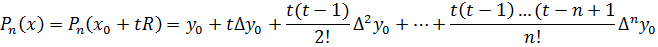
| X | 0. 5 | 1. 5 | 2. 5 | ||
| y | 1. 715 | 2. 348 | 3. 127 | 5. 289 | 8. 914 |
1 способ:
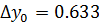
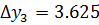
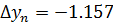
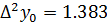
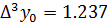
2 способ:
|
|
|
|
|
|
|
|
|
|
|
|
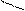
воздух
вода
I- Компрессор
II- Камера сгорания
III- Газовая турбина
IV- Паровой котел
V- Пароперегреватель
VI- Паровая турбина
VII- Конденсатор
VIII- Насос
IX- Регенеративный перегреватель
X- Водяной экономайзер
XI- Генератор
XII- Генератор
Сжатый воздух подаётся на компрессор 1. С него воздух поступает в камеру сгорания, с камеры сгорания поступает на газовую турбину. Турбина вырабатывает механическую энергию, которая запускает электрогенератор, вырабатывающий электрическую энергию уходящих газов. Затем подаётся на паровой котел, который вырабатывает влажный пар. Перегретый пар подаётся на паровую турбину, которая вырабатывает механическую энергию. Отработанные газы подаются на регенеративный подогреватель, где греют воду. Влажный пар поступает на конденсатор 7, где пар преобразуется в воду. Образовавшаяся вода насосом 8 подаётся на подогреватель 9 и водяной экономайзер 10. В нем вода подогревается и подаётся на паровой котел 4.
|
|
|
Носители:
1) Воздух
2) Топливо (газ)
3) Продукты сгорания
4) Перегретый пар
5) Влажный пар
6) Вода
7) Отработанные газы
8) Уходящие газы
9) Электрическая энергия
10)Механическая энергия
Продолжение лекций
1. Общий расход свежего пара на станции:
N- число турбоагрегатов, участвующих в распределении электрической нагрузки.
2. Общий расход топлива на электростанции:
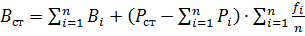(14)
n- Количество параллельно работающих агрегатов
3. Расход питательной воды:
n- Количество параллельно работающих подогревательных установок.
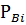- расход воды
- энтальпия соответствующей установки
Ограничивающими условиями для (15) является постоянство общего расхода свежего пара на станции и питательной воды.
Расчёт приращения функции Лагранжа с использованием полученных зависимостей. Для множителей Лагранжа задаваемых по формуле (11) дает возможность определить последовательность загрузки и разгрузки отдельных агрегатов.
Загружаются в первую очередь агрегаты, для которых получено наименьшее приращение функции Лагранжа. 
. Разгружаться должны с наибольшим приращением. Следует учитывать, что сумма приращений по нагрузке каждого агрегата не обязательно =0.
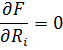
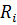- нагрузка i-ого агрегата.
В этом случае режим распределения нагрузки будет моделироваться следующей системой уравнений:
Система: (16)
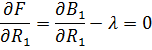
Перенесём 
в правую часть, и провести суммирование частей:
Для неограниченного множителя Лагранжа:
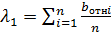(17)
Уравнение (17) получено в предположении, что изменение каждого вида нагрузки носит независимый характер. Это справедливо только при распределении конденсационной выработки энергии, то есть при определении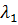 
. При распределении производственного пара и тепловой нагрузки изменяется электрическая мощность турбоагрегатов, что скажется при определении 
.
|
|
|
Таким образом, для оптимизации расходов пара от каждой из турбин с учётом изменяющейся выработки электрической энергии получена система уравнений:
Система: (18)
.
.
.
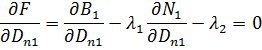
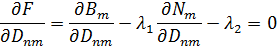
Если перенести и просуммировать части уравнения получили:
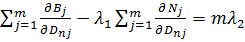(19)
m- Блоки, вырабатывающие пар.
(20)
Аналогично для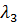 
:
(21)
r- Блоки, участвующие отоп. параметров.
Таким образом, рассчитываемые зависимости для определения множителей Лагранжа в уравнении (7) будут иметь следующий окончательный вид:
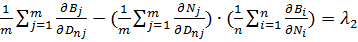(22)
При расчётах приращения функции 
обусловленных изменением каждого из видов нагрузки с учётом функции (22) получим следующее:
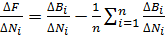
(23)
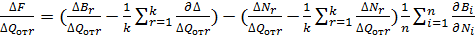
Определение нагрузок между парогенераторами энергоблока при сжатии нескольких видов топлива.
На практике на функционирующих станциях используются два и более видов топлива. Как правило это применяется на ТЭЦ нефтехимических комбинатов, где целесообразно кроме основного топлива использовать побочные продукты производства.
При этом возможно 2 способа совместного использования:
1. Совместное сжатие двух видов топлива в котлоагрегата. В частности используется для обеспечения устойчивого факела на комплексных нагрузках при сжатии низко реакционных ушей.
2. Сжатие каждого вида топлива в различных котлоагрегатах может быть обусловлено стремление получить максимального КПД или технической не приспособленностью отдельных котлоагрегатов для совместного сжатия различных видов топлива.
В случае раздельного использования или ограниченного расход одного из них, ограничение задается либо на суточных периодах, либо в отдельные часы. Обычно задается определенный расход топлива в часах суток.
|
|
|
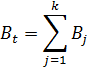
С учетом ограничений часового расхода одного из видов топлива, а также общей нагрузки станция для группы параллельно работающих генераторов функция Лагранжа запишется следующим образом:
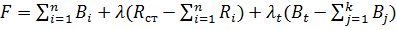(24)
k- Количество агрегатов, работающих на ограниченном топливе.
n- Общее количество агрегатов.
Задача оптимизации распределения нагрузки имеет два этапа:
1. Заключается в определении оптимальных мощностей агрегатов, работающих на ограниченном топливе. Условие достижения оптимума в данном случае является достижение суммарной мощности установки, потребляющей данный вид топлива.
Для этой группы функция Лагранжа записывается:
(25)
Если продифференцировать функцию по каждой из к-ых переменных, то получим систему:
Система: (26)
.
.
.
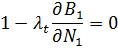
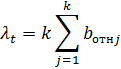
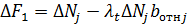
Для достижения максимальной суммарной мощности необходимо увеличить в механическом агрегате, где 
, и снижать для которых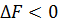 
.
2. Этап заключается в оптимальном распределении нагрузок между оставшимися агрегатами, работающим на замыкающем, неограниченном топливе.
Для этой группы агрегатов функция Лагранжа запишется:
|
|
|
