 |
Распределение тепловых и электрических нагрузок на ТЭЦ.
|
|
|
|
Наиболее распространенным типом теплофикационных электростанций является промышленно оптимальная ТЭЦ отдающая потребителям из отборов производственный пар под давлением от 0, 7 до 1, 3 МПа. И горячую воду подогреваемую паром из теплофикационных отборов, а также вырабатывающую электрическую энергию.
Электроэнег. Потреб.
Здесь устанавливаются турбины типа ПТ, Р, Т их можно объединить в соответствующие подгруппы, а именно:
По виду отдаваемой энергии:
· Осуществляется отпуск электрической энергии (1-4 турбины);
· Отпуск пара производственных параметров (1, 2, 3);
· Отпуск пара теплофикационных параметров (1, 2, 4)
Для каждой с производной энергией записывается следующее ограничительное уравнение.
Nст= 
; 
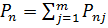
-отпуск пара производственных параметров, кг/с
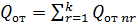(6)
- отпуск низкопотенциального тепла полученного за счёт пара теплофикационных параметров, Дж/с
В соответствии с уравнением связи функция Лагранжа будет записана следующим образом.
(7)
Количество уравнений в системе описывающих функционирование станций равняется сумме агрегатов во всех группах 4+3+3+3 уравнения связи.
При решении задач оптимизации должны учитываться ограничения по предельным значениям отпуска тепловой и электрической энергии.
По максимальному расходу свежего пара и по минимальной электрической мощности определяют тепловой нагрузкой агрегатов. Решение задачи распределения нагрузок в масштабе энергосистемы большого количества агрегатов приводит к большому числу расчётных уравнений и делает расчёт сложным. Поэтому на практике решается в пределах одной станции.
|
|
|
Для нахождения минимума функции применяется градиентный метод. Суть метода заключается в следующем: исходно принимается вариант распределения нагрузок между энергоблоками станции с соблюдением существующих ограничений, затем для минимизируемой функции, которая представляет собой функцию переменных.
F(x1; x2; …xn)
Определяем приращение вызванное изменением каждой переменной.
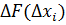
Шаг расчёта осуществляется в направлении убывания функции F, что соответствует такому изменению параметра xi, при котором 
должна иметь обратный знак. Поиск оптимального решения заканчивается условием:
,
Где 
- величина заданной точности решения.
Расчёт отношений при варьировании каждой из переменных требует предварительного определения множителей Лагранжа: 
.
Расход топлива комбинированной энергоустановки, участвующей в отпуске энергии, паропроизводственных параметров определяется следующим образом:
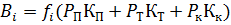(8)
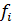- удельный расход топлива на единицу свежего пара, кг топлива/кг пара.
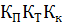- коэффициент учитывающий расход пара на подогрев питательной воды, численно равный соответствующим отношениям расходов свежего пара к расходам, в производственный отбор, отопительный отбор, отопительный теплофикационный отбор, конденсатор.
- расход пара в отопительные отборы, кг/с
В данном случае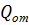 
- суммарный отпуск теплоты на станции.
- количество теплоты отдаваемой 1 кг пара поступавшего в отборы, кДж/кг.
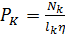– расход пара в конденсаторе, кг/с;
– мощность, выработанная конденсатором, кВт;
- полезная работа совершаемая 1 кг пара поступавшего в конденсатор турбины, кДж/кг;
- электромеханический КПД;
|
|
|
Выражая каждый расход пара через соответствующие электрические и тепловые мощности, получим для расхода топлива выражение:
Тогда функция Лагранжа примет вид:
Сравним (7) и (10) сможем записать значения множителей Лагранжа:
Система: (11)
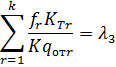
В нашем случае множителем Лагранжа представляют собой усредненное значение удельных расходов на выработку соответствующего вида энергии для рассматриваемой группы энергоагрегатов в каждую из подгрупп входят агрегаты, участвующие в параллельном отпуске заданного вида энергии и имеющие соответствующий регулировочный диапазон.
Отсюда следует 2 вывода:
1) Изменение отпуска данного вида энергии компенсируется соответствующим изменением нагрузки всех агрегатов подгрупп;
2) Условия оптимального распределения выработки энергии достигается, когда приращение удельного расхода топлива вследствие изменения нагрузки каждого из агрегатов приближается к среднему удельному расходу топлива в подгруппе. Это соответствует первоочередной загрузке установки с меньшими относительными приростами расхода топлива.
Для получения точного результата с использованием функции (10) следует учитывать, что увеличение отпуска теплоты какими-либо агрегатами.
как правило, приводит к росту энергетической мощности генерируемой агрегатом одновременно, уменьшится отпуск тепла от других установок.
Соответственно уменьшается и вырабатываемая ими электрическая энергия. Результирующее изменение теплофикационной турбины по мощности:
В качестве проверки правильности расчёта можно рассматривать соблюдения равенства сумм величин с отрицательным и положительным приращением.
Оптимизация распределения нагрузок на ТЭЦ имеющие поперечные связи по пару и питательной воде отличается тем, что общая задача оптимизации делится на ряд подзадач, в которых рассматривается ряд частных решений:
Подзадачи:
· Распределение тепловых и электрических нагрузок по минимуму расхода электричества на нагрев пара на ТЭЦ;
· Распределение выработки пара между отдельными агрегатами по минимум расхода топлива на станции;
· Распределение расхода питательной воды по подогревателям высокого давления из условий достижения максимальной энтальпии.
|
|
|
Таким образом, соответствующие этим задачам функции будут иметь вид:
1. Общий расход свежего пара на станции:
|
|
|
