 |
Моделирование тепловых полей.. Начальные и граничные условия.
|
|
|
|
Моделирование тепловых полей.
Объектом моделирования является тепловые компоненты, определяющие перенос тепла от одних участков к другим. В фиксированный момент времени тепловые компоненты определяют распределение температуры по телу.
T=T(x, y, z, t)- декартовы координаты.
В простейшем случае тепловой поток из области более высокой температуры в область более низкой.
Три способа переноса тепла:
· Теплопроводность (взаимодействие микрочастиц соприкасающихся тел);
· Конвекция (перенос, обусловленный пространственным перемещением вещества в движущихся средах);
· Излучение (перенос в виде электромагнитных волн);
В реальном случае имеем все 3 случая- сложный теплообмен.
Математическое описание даётся уравнением. Основное положение теплопроводности закон Фурье. Заключается в предположении пропорциональности теплового потока градиенту температур в одной не подвижной среде.
Закон сохранения энергии для процесса передачи тепла:
(1)
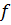определяет мощность внутренних источников тепла. Если подставленное в функцию (1) выражение для потока тепла, то получим уравнение теплопроводности.
(2)
Все коэффициенты и f в общем виде в случае неоднородной среды будет зависеть от точки пространства.
cp=cp(x, y, z)
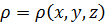
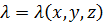
Кроме того эти величины в локальной точке будут так же зависеть от температуры.
Если подставить в уравнение (2), то получим уравнение теплопроводности в квазилинейной форме. Это уравнение основа для моделирования тепловых полей.
Частные случаи:
1) Однородная среда. Дифференциальное уравнение определяется формулой (2) и запишется:
|
|
|
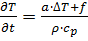(3)
a- Коэффициент температуропроводности.
2) Стационарное уравнение теплопроводности. Оно описывает состояние установившихся тепловых полей.
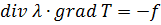(4)
3) Моделирование переноса тепла в движущейся среде в этом случае уравнение теплопроводности:
(5)
В случае отсутствия внутренних тепловых источников f=0 уравнение имеет вид:
(в декартовой системе)
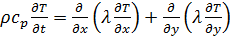(6)
(в полярной системе)
X=r cos 
Y=r sin 
(7)
T=T(r, 
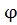, t)
Начальные и граничные условия.
Распределение температуры в точках среды в различных моментах времени определяем из уравнения частных производных.
Для определения температурного поля необходимо уравнение теплопроводности и сформулировать исходные условия и граничные условия.
Исходным условием будет функция:
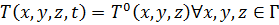
Справедливо для всех x, y, z в области решения уравнения.
Граничные условия 1 рода задаётся исходное определение температуры.
Справедливо для декартовых координат.
Граничные условия 2 рода определяются заданием на границе исследуемой среды теплового потока.
 | ||||||||||||
 | ||||||||||||
 | ||||||||||||
| ||||||||||||
 | ||||||||||||
| | ||||||||||||
| | ||||||||||||
| |
| |||||||||||
| ||||||||||||
X=0
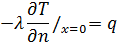
q> 0
q< 0
Если q> 0 происходит нагрев области, а если q< 0 происходит охлаждения.
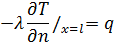
Граничные условия 3 рода моделирует конвективный теплообмен между поверхностью твердого тела и окружающей средой, имеет поверхностную температуру 
на границе х=0:
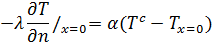
Условия 4 рода – условия сопряжения. Они устанавливаются на границе контакта 2 сред с различными теплофизическими характеристиками.
|
|
|
 |
Система:
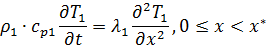
T-температура
t-время
В случае идеального компонента.
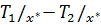
На практике имеет место не идеальный контакт сред с различными теплофизическими свойствами. Соприкосновение шероховатых твердых тел.
Температура не меняется, тепловой поток неразрывен.
- коэффициент контактного теплообмена, который связан с условиями осуществления контакта.
Одномерная задача теплопроводности для неоднородного стержня:
0
1
Z1
2 z2
3 L
L
Задача описывается уравнением:
Система:
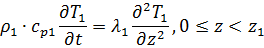
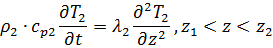
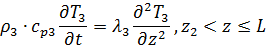
Начальные и граничные условия в нашем случае запишем следующим образом:
t=0
T(t)=T0
0< =z< =L
Z=0
Z=L
Условия 3 рода определяют границу:
Система:
T1(t, z1)=T2(t, z1)
Условия для границе 2 и 3 областей соответственно:
Система:
T2(t, z2)=T3(t, z2)
Для численного решения осуществляют построение численной сетки.
Шаг по пространственной координате:
N-количество отрезков разбиения на оси z.
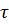-шаг по времени.
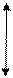
Z1
h
Z2
Zi-1
h
zi
L zn
Z1=0
Z2=h
Zn-1=(N-2)h
Zn=(N-1)h=L
tn=n 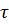; n=0, 1…
T(zi, tn)=Tin
После построения разностной сетки можно провести дискретизацию дифференциального уравнения частных производных. Исходя из величин конечной разности получаемых при задании сетки.
i- Пространство
n- Время
С учётом дискретизации получаем:
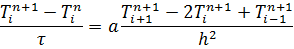
a- Коэффициент температуропроводности
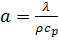(1)
|
|
|
Полученное уравнение решается методом прогонки. Для этого приводим к следующему виду.
(2)
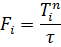
Решение уравнения (2) осуществляется с использованием формулы прогонки
Понизим индекс на единицу:
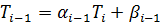
(3)
Для использования формулы (3) необходимо определить начальные прогоночные коэффициенты 
.
Они определяются использованием левого граничного условия 2 рода.
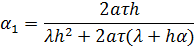
После определения стартовых значений используем метод прогонки по формуле (3) определяем значения для всех узлов пространственной сетки за исключение узлов в соответствии напряжения соприкосновения материалов имеющие различные теплофизические свойства. В этих узлах коэффициенты определяются с использованием граничных условий 4 рода.
Исходя из условий 4 рода:
Для 1 и 2 сред.
Для 2 и 3 сред:
|
|
|
