 |
Топологическое моделирование теплоэнергетических установок.
|
|
|
|
Топологическое моделирование теплоэнергетических установок.
Для решения задач математического моделирования анализа и оптимизации систем применяется 4 класса графов.
1. Потоковый Граф;
2. Информационные потоковые графы;
3. Сигнальные графы;
4. Структурные графы;
Атака Граф отображает особенности технологическая топология система установок связь между изменением технологической топологии и количественными характеристиками системы.
Потоковые графы делятся:
· Параметрические
· Материальные
· Тепловые
· Эксергетические
Применяется для разработки алгоритмов оптимальной стратегии расчёта систем. Информационно потоковый граф отражает особенности информационной структуры системы уравнений, математической модели.
Сигнальные графы отображают причинно-следственные свойства между переменными и параметрами линейной системы уравнений, математической модели. Они используются для решения многомерных систем уравнений и для расчёта показаний устойчивости, чувствительности и надежности системы.
Структурные графа отображают особенности физико-химических явлений протекающих в системе:
· Гидравлические
· Тепловые
Основы теории графов.
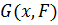задана если задано не пустое множество точек 
и многозначное отображение F этого множества.
Элементы множества изображаются точками и называются вершинами графа. Отображение F изображается отрезками между соответствующими элементами, и называются ребрами или векторами (дугами). Нуль графа, состоящий из изолированных вершин.
| |||||||||||||
 | |||||||||||||
| |
| ||||||||||||
| |||||||||||||
| |||||||||||||
| | | ||||||||||||
| |||||||||||||
| | |||||||||||||
|
|
|
Граф, в котором все вершины соединяются ребрами, называется неориентированным графом. Граф, в котором все вершины соединены не только ребрами, но и дугами, называется ориентированным графом.
Дуги- вектора задающие направление.
Две вершины графа смежные, если они определяют ребро или дугу. Две дуги смежные, если имеют общую вершину.
Каждой изолированной вершине подходит одна или несколько дуг, которые называют инцидентными данной вершине.
В графах выделяют типовые фигуры, а именно:
1. Путь последовательных дуг между парой вершин, в которой один конец дуги является началом другой.
2. Контурно-замкнутый путь, в котором начальные и конечные вершины совпадают.
3. Петля элементарный контур единичной длины.
В неориентированных графах выделяют:
· Цепь- непрерывная последовательность ребер между любой парой вершин.
· Цикл- замкнутая цепь.
· Взвешенный граф- ребра или вершины, которого имеют определенный вес в виде чисел, значений или коэффициентов.
· Мультиграф- некоторые пары вершин, которые могут быть соеденины более чем одним ребром.
· Дерево- связный граф, в котором любая пара вершин соединена только одной связью.
· Связный граф- граф между всеми элементами есть связи.
Используют следующие характеристики графа:
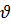- число вершин;
- число ребер, дуг или ранг графа;
K- число связанных компонентов не связанного графа.
минимальному числу ребер удаление которых из графов приводит к образованию дерева.
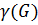- число вершин связанности
минимальному числу вершин графа, удаление которых из графа приводит к образованию не связного или тривиального графа, когда нет связи между всеми элементами.
- число реберной связности. Минимальное число ребер, удаление которых приводит к образованию не связного или тривиального графа.
|
|
|
