 |
Задача о максимальном потоке. Задача о кратчайшем пути. Задача о назначениях. Матрица соединений. Матрица связей. Матрица смежности
|
|
|
|
Задача о максимальном потоке.
Пусть имеется некоторая сеть с определённой пропускной способностью dij из I-ой в j-ый узел необходимо так организовать перекрещение или носителя по сети, чтобы его максимальное количество было перемещено изначально узлов конечный узел. Обозначим переносное количество xij I, j=1…n. Математическая постановка о максимальном потоке сформулирована следующим образом:
Система:
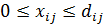
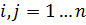
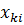- количество энергоносителя в i-ом узле.
Задача о кратчайшем пути.
Пусть имеется сеть с источником Sи потоком t. Известно расстояние между i-ой и j-ой вершиной расстоянием Cij. Необходимо найти кратчайший путь из начального узла в конечный узел.
Система:
Целевая функция
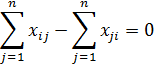
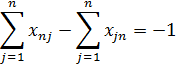
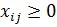
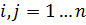
Первое ограничение означает, что единица потока вытекает из источника S. Третье ограничение означает, что единица потока втекает в сток t. Второе ограничение означает, что при протекании через сеть величина потока сохраняется.
- Булева переменная, она равна 1, если узел лежит на кратчайшем пути, и равна нулю, если не лежит на кратчайшем пути.
Задача о назначениях.
В общем виде формулируется:
Пусть имеется m работ и nкандидатов для их выполнения причём назначение i-ого кандидата на j-ую работу соответствует определенный результат.
Требуется найти также назначения кандидатов на все работы, которые обеспечат наилучший результат. Кандидат может быть назначен на выполнение 1 работы. Математическая постановка задачи.
Max или min L=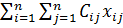 
Система:
- искомая переменная вероятность назначения i-ого работника на j-ую работу.
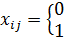
Это постановка задачи относятся к классу комбинаторных задач. При большом количестве работы кандидатов она не может быть решена методом перебора вариантов, так как количество возможных вариантов назначение N работ и работников N!
|
|
|
Венгерский метод.
Известно несколько различных методов решения комбинаторных задач. Наибольшее распространение получили венгерский метод. Основная идея заключается в том, что оптимальность решения задачи не нарушается при уменьшении или увеличении элементов строк и столбцов матрицы, представляющий собой исходное условие задачи на одну и ту же величину.
Решение считается оптимальным, если все вероятности назначений Cij считается ³ 0, где i, j=1…n можно отыскать набор xij, что
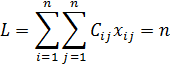
Упражнения: построить матрицы для графов:
Матрица соединений
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
| -1 | |||||||||||
Матрица связей
Матрица смежности
|
|
|
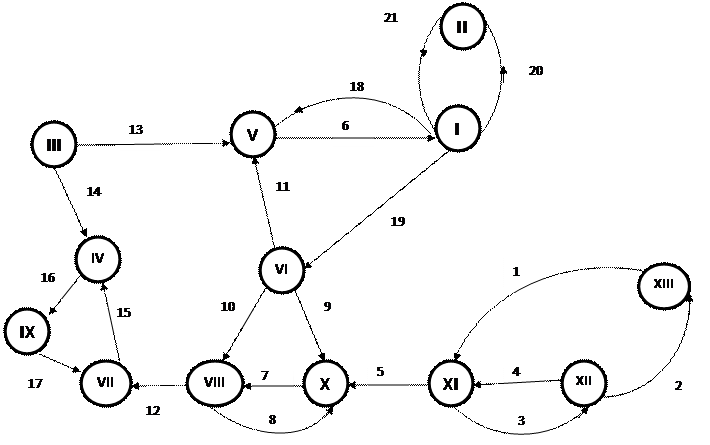
Матрица достижимости и контрдостижимости строки и столбцы элементов в графе.
1- Если есть прямой путь между i-ой и j-ой вершиной;
0- Если нет пути;
Контрдостижимости
0- Если нет обратного пути;
1- Если есть обратный путь;
Достижимости
Контрдостижимости
Лекции продолжение
Рассмотрим пример. Пусть необходимо осуществить монтаж и объектов и работников известно время монтажа каждым i-ым работником j-ого объекта. Необходимо распределить работников по объектам, чтобы суммарное время монтажа было минимальным. Затраты времени, Cij.
|
|
|
| N | ||||
Формальная постановка задачи:
Система:
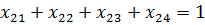
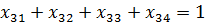
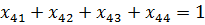
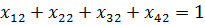
Алгоритм метода включает основные этапы:
1. Получение нулей в каждом строке.
1. 1. Находим наименьший элемент в каждой строке и вычитаем его из всех элементов для получения новой матрицы.
1. 2. Аналогичным образом в каждом столбце определяем его минимальный элемент, который вычитают из всех элементов с получением следующей матрицы.
 1
| 0* | |||
 2
| Æ | 0* | Æ | |
| 0* | 2Ö | |||
| Æ | 2Ö |
2. Поиск оптимального решения.
2. 1. Рассматривается одна из строк имеющая меньше число нулей. Например, строка 1 отмечается звёздочкой один из нулей этой строке. Затем зачеркиваются все остальные нули этой строки этого столбца, в котором отмечен и находится отмеченный звездочкой 0.
2. 2. Аналогичная операция выполняется последовательно для всех строк.
2. 3. Если значения, которые получены при всех нулях отмеченных звездочкой являются полными, то есть число отмеченных звездочкой нулей равняется N, то решение является оптимальным. В противном случае переходим к шагу 3.
3. Поиск минимального набора строк и столбцов, содержащих нули.
3. 1. Отмечают:
3. 1. 1. Все строки, в которых нет ни одного отмеченного звездочкой 0 ( строка 4).
3. 1. 2. Все столбцы, содержащие перечеркнутый 0, хотя бы в одной из отмеченных строк (столбец 3).
3. 1. 3. Отмечают все строки, содержащие отмеченные звездочкой нули, хотя бы в одном из отмеченных столбцов (строка 3).
3. 2. Шаги 3. 1. 2. и 3. 1. 3. Повторяют поочередно до тех пор, пока есть что отмечать.
3. 3. Зачеркивает каждую не помечена строку, и каждый помечены столбец (строка 1, 2 и столбец 3), чтобы получить минимальное количество горизонтальных и вертикальных прямых, пересекающих один раз все нули.
4. Перестановка некоторых нулей определяет наименьшее число из тех меток, через которые не проведены прямые которые не зачеркнуты (число 2), это число вычитается из каждого числа не вычеркнутых столбцов и прибавляются каждому числу вычеркнут из строк на пересечении с вытянутыми столбцами, таким образом, получают новую матрицу, если это операция не приводит к оптимальному решению начиная со второго шага, то продолжается до получения оптимума.
|
|
|
| 0* | ||||
| Æ | 0* | Æ | ||
| Æ | 0* | |||
| Æ | Æ | 0* |
Это значит, что вероятность:
|
|
|
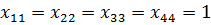
