 |
Основы статистического моделирования технических систем.
|
|
|
|
Метод статистического моделирования м. Monte Carlo способ исследования поведения технических вероятностных систем.
В условиях, когда неизвестный в полной мере внутреннее взаимодействие этих систем. Этот метод заключается в воспроизведении исследуемого физического процесса при помощи вероятностные математической модели и вычисления характеристик этого процесса. Такое воспроизведение функции системы реализация или испытанием. После каждого испытания регистрируются совокупность параметров характеризующих случайно исход реализации. Метод основан на многократных испытаниях построены модели с последующим статической обработкой полученные данные с целью определения числовых характеристик рассматриваемого процесса в виде статических оценок его параметров. Процесс моделирования свойства к математической имитации изучаемого процесса, который конструируется на ЭВМ сопровождением его случайности.
Метод Монте-Карло разработан в конце сороковых годов 20 века.
Существенный вклад внесли в пятидесятых Чавчавадзе, Шрейдером, Владимировым.
Основы методов статистического моделирования является закон больших чисел. Теория вероятности доказывают для различных условий сходимость по вероятности средних значений, результатов большого числа наблюдений и некоторыми постоянными величинами.
Закон больших чисел объединяет несколько теории Чебышева и Бернулли. Chebyshev: при неограниченном увеличении числа независимых испытаний N среднее арифметическое от систематических ошибок равноточных результатов наблюдений zi случайные величины z, имеющие конечную дисперсию  сходится по вероятности по математическому ожиданию и случайную величину.
сходится по вероятности по математическому ожиданию и случайную величину.
|
|
|
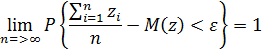
 - Точность заданных измерений.
- Точность заданных измерений.
Теорема Бернулли: при пограничном увеличении числа неизвестных испытание в одних и тех же условиях частота наступления случайного события А сходится к вероятности.

 - неизвестная исследуемая величина.
- неизвестная исследуемая величина.
Вычисляется частота одной реализации: 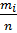 ;
;
Осуществляя вычисление для количества реализации равного N. Результаты устраняется результате с некоторым приближением Эпсилон получает искомые вероятности состояния системы. На основании вычисленных вероятностей определяют физические и технические характеристики систем. Алгоритм решения любой задачи методом статистического моделирования состоит в следующем:
1. Разработка и построение структурной схемы процесса выявления основных взаимосвязей.
2. Формальное описание процесса.
3. Моделирование случайных явлений ( случайных событий, величин, функций) сопровождающей функционирования исследуемой системы. Произведение процесса в соответствии с разработанной структурной схемой и формальным описанием.
5. Наполнение результатов моделирования, статистическая обработка, анализ и обобщение.
В отличие от математического моделирования, результаты которых отражали устойчивое поведение системы, результаты, полученные при моделировании подвержены эксперименту.
Упражнения
Матрица пересечений

Матрица квадратная число строк и столбцов равно числу элементов в графе.
0- Если между i-ой и j-ой вершиной нет прямого или обратного пути.
1- Если между i-ой и j-ой вершиной есть прямой или обратный путь.
|
|
|
Матрица контуров на дугах

Строками является количество контуров, в графе столбцы количество дуг в графе.
0- Если j-ая не принадлежит i-ому контуру
1- Если j-ая принадлежит i-ому контуру

Матрица контуров на вершинах

Столбцы - вершины
Строки – контуры
0- Если j-ая вершина не входит в контур
1- Если j-ая вершина входит в контур
Определить критический путь и все возможные резервы для всех работ:
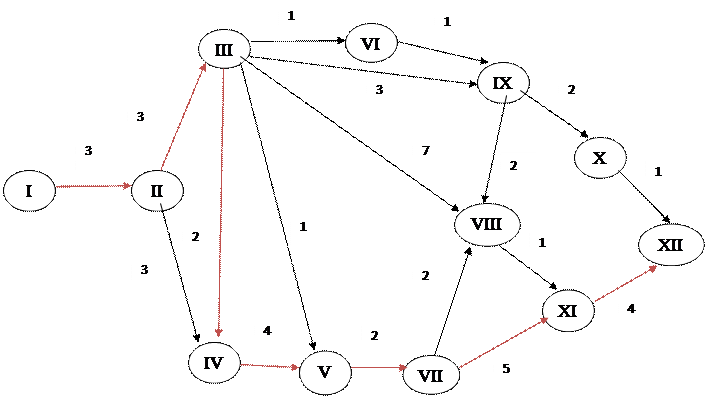
|
|
|


