 |
Вопросы для обсуждения. ТЕМА №3. Числовые характеристики распределений. Нормальное распределение. 3.1. Мода и медиана. Среднее арифметическое.
|
|
|
|
Вопросы для обсуждения
1. Дайте определение генеральной совокупности и приведите примеры генеральных совокупностей. Каков объём генеральной совокупности?
2. В чём заключается полное психологическое исследование? В каких случаях оно возможно? В чём преимущество и недостатки такого исследования?
3. Выборка и её объём. Репрезентативность выборки. Респондент. Выборочное исследование.
4. В чём различие между понятиями «независимые выборки» и «несвязные выборки»? Между «независимые выборки» и «зависимые выборки»?
5. В вашей группе проведены два исследования: на выявление мотивов учения и определение типа темперамента. Со сколькими выборками пришлось в данном случае работать исследователю?
6. Что называется группировкой экспериментального материала? Каковы возможные виды группировки?
7. Каковы отличия простых статистических таблиц от сложных? Как проверить правильность составления данных таблиц?
8. Что называется статистическим рядом?
9. Что называется вариантой, её частотой и относительной частотой?
10. Как представить относительную частоту в процентах? Как проверить правильность составления статистического ряда?
11. Многопольные таблицы. Приведите пример четырёхпольной, восьмипольной таблиц. Может ли таблица быть семипольной?
ТЕМА №3. Числовые характеристики распределений. Нормальное распределение.
3. 1. Мода и медиана. Среднее арифметическое.
Для экспериментальных данных, полученных по выборке, можно вычислить ряд числовых мер. Это мода, медиана, среднее арифметическое, разброс выборки, дисперсия, стандартное отклонение.
Мода – такое числовое значение, которое встречается в выборке наиболее часто. Обозначается иногда как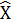 
(или Мо ).
|
|
|
Пример 3. 1. Определить моду в ряду значений: (2, 6, 6, 8, 9, 9, 9, 10).
Решение: модой является число 9, т. к. 9 встречается чаще других значений. 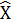= 9.
Правила нахождения моды
1) Если все значения в выборке встречаются одинаковое число раз, говорят, что выборочный ряд не имеет моды.
2) Когда 2 соседних (смежных) значения имеют одинаковую частоту и их частота больше частот любых других значений, мода вычисляется как среднее арифметическое этих значений.
Пример 3. 2. Имеется ряд значений: (1, 2, 2, 2, 5, 5, 5, 6). Частоты смежных значений 2 и 5 совпадают и равны 3. Эта частота больше, чем частота других значений 1 и 6. Следовательно, модой этого ряда будет величина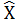 
= 3, 5.
3) Если два несмежных (не соседних) значения в выборке имеют равные значения, которые больше частот любого другого значения, то выделяют две моды. В этом случае выборку называют бимодальной. Могут существовать и мультимодальные ряды.
Медиана – это значение, которое делит упорядоченное множество данных пополам. Обозначается как 
(или Md ).
Пример 3. 3. Найти медиану выборки: 9, 3, 5, 8, 4, 11, 13.
Решение: Сначала упорядочим выборку по величинам входящих в неё значений: (3, 4, 5, 8, 9, 11, 13). В выборке 7 элементов, следовательно, четвёртый по порядку элемент (8) будет средним (до него – 3 элемента и после него 3 элемента). Таким образом, медианой будет четвёртый элемент: =8.
Пример 3. 4. Найти медиану выборки: 20, 9, 13, 1, 4, 11.
Решение: Упорядочим выборку: (1, 4, 9, 11, 13, 20). Поскольку имеется чётное число элементов, то существует две «середины» - 9 и 11. В этом случае медиана определяется как среднее арифметическое этих значений:
= 
= 10.
Среднее арифметическое ряда из n числовых значений Х1, Х2, … Хn обозначается 
(икс с чертой) и вычисляется как:
= 
= 
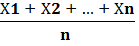(Σ Хi)
В том случае, если отдельные значения выборки повторяются, среднюю арифметическую вычисляют по формуле:
|
|
|
= 
(Σ xi fi), где fi – частоты повторяющихся значений.
в таком случае называют взвешенной средней.
Средние величины характеризуют выборку одним (средним) числом. Их преимущество состоит в способности уравновешивать все индивидуальные отклонения, в результате чего проявляется то наиболее устойчивое и типичное, что характеризует качественное своеобразие варьирующего объекта, отличает данную выборку от другой. Однако, среднее как статистический показатель не лишено недостатков. Поэтому в статистике, кроме средней величины, используются и другие характеристики «типичных значений» - мода и медиана.
|
|
|
