 |
3.2. Разброс выборки, дисперсия, стандартное отклонение.
|
|
|
|
3. 2. Разброс выборки, дисперсия, стандартное отклонение.
Кроме величин, характеризующих типичные значения выборки (мода, медиана, средние значения), существуют числовые характеристики выборочного ряда, позволяющие определить степень варьирования (изменения) измеряемого признака. Это разброс выборки, дисперсия и стандартное отклонение.
Разброс (размах) выборки – это разность между максимальной и минимальной величинами данного конкретного вариационного ряда:
R = Xmax - Xmin
Чем сильнее варьирует измеряемый признак, тем больше величина R, и наоборот.
Однако бывает, что у двух выборочных рядов и средние, и размах совпадают, а характер варьирования рядов различен. Данный факт подтверждается такими числовыми характеристиками как дисперсия и стандартное отклонение.
Дисперсия – среднее арифметическое квадратов отклонений значений переменной от её среднего значения.
D = 
, где n – объём выборки, 
Дисперсия обозначается символами D (по генеральной совокупности) или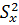 
(по выборке).
Стандартное отклонение – величина, равная квадратному корню из дисперсии: σ =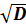 
.
Стандартное отклонение по выборке обозначается Sx. Другое название стандартного отклонения: среднее квадратическое отклонение.
3. 3. Число степеней свободы.
Число степеней свободы (n) – это число свободно варьирующих единиц в составе выборки. Оно равно числу классов вариационного ряда минус число условий, при которых он был сформирован. К числу таких условий относятся объём выборки (n), средние и дисперсии.
Число степеней свободы у выборочного ряда определяется:
n = n – 1, где n – общее число элементов ряда (выборки).
При наличии не одного, а нескольких ограничений свободы вариации, число степеней свободы определяется по формуле:
|
|
|
ν = n – k, где k – число ограничений свободы вариации.
Для таблицы экспериментальных данных число степеней свободы определяется следующим образом:
ν = (c – 1) (n – 1), где c – число столбцов, а n – число строк таблицы (число испытуемых).
Для ряда статистических методов подсчёт числа степеней свободы оказывается необходимым и рассчитывается по-своему.
3. 4. Понятие нормального распределения.
В статистике под рядом распределения понимают распределение частот по вариантам. Распределением признака называется закономерность встречаемости разных его значений.
Особое место в статистике занимает нормальное распределение. График нормального распределения представляет собой колоколообразную кривую. Форма и положение графика определяется только двумя параметрами: средней (µ) и стандартным отклонением (σ ).
Для нормального распределения характерно совпадение величин средней арифметической, моды и медианы. Равенство этих показателей указывает на нормальность данного распределения.
Ещё одна особенность нормального распределения: чем больше величина признака отклоняется от среднего значения, тем меньше будет частота встречаемости (вероятность) этого признака в распределении. «Нормальным» распределение названо потому, что оно наиболее часто встречалось в естественнонаучных исследованиях и казалось «нормой» распределения случайных величин.
| -4σ |
| -3σ |
| -2σ |
| -σ |
| μ σ 2σ 3σ 4σ |
В психологии нормальное распределение используется при разработке и применении тестов интеллекта и способностей. Для показателей интеллекта IQ нормальное распределение имеет µ = 100, а σ = 16 для большинства возрастных групп.
|
|
|
Однако, для других психологических категорий (личностная и мотивационная сфера) применение нормального распределения оказывается дискуссионным.
При нормальном распределении экспериментальных данных применяются особые методы статистической обработки.
Кроме нормального существуют и другие распределения. При обработке экспериментальных данных целесообразно проводить оценку характера распределения. Это поможет решить вопрос о возможности применения того или иного статистического метода.
|
|
|
