 |
Ответ: 2634240 рублей. 5 тип: Нахождение разницы. (Аннуитетные платежи). 3 равных платежа. 3 равных платежа Год Долг с % Платеж Долг после выплаты
|
|
|
|
Ответ: 2634240 рублей.
5 тип: Нахождение разницы. (Аннуитетные платежи)
Задача №1.
31 декабря 2014 года Федор взял в банке 6951000рублей в кредит под 10% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Федор переводит в банк платеж. Весь долг Федор выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?
Решение:
Сумма кредита S = 6951000 рублей
Ставка r = 10%, р = 1, 1
3 равных платежа
| Год | Долг с % | Платеж | Долг после выплаты |
| S | |||
| 1 год | Sр | x | Sр – x |
| 2 год | (Sр – x)р = Sр2 – рx | x | Sр2 – xр – x |
| 3 год | р(Sр2 – xр – x) = Sр3 – хр2 – xр | x | - |
Sр3 – хр2 – xр = х
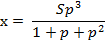
х = 2795100
2 равных платежа
| Год | Долг с % | Платеж | Долг после выплаты |
| S | |||
| 1 год | Sр | x | Sр – x |
| 2 год | (Sр – x)р = Sр2 – рx | x | - |
Sр2 – рx = х
Sр2 = рx + х
Sр2 = х(р + 1)
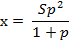
Подставим и сосчитаем х
х = 4005100
За три года: 2795100 · 3 = 8385300
За два года: 4005100 · 2 = 8010200
Разница: 8385300 – 8010200 = 375100
Ответ: на 375100 рублей.
Задача №2.
31 декабря 2014 года Степан взял в банке 4004000 рублей в кредит под 20% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Степан переводит в банк платеж. Весь долг Степан выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?
Решение:
Сумма кредита S = 4004000 рублей
Ставка r = 20%, р = 1, 2
3 равных платежа
| Год | Долг с % | Платеж | Долг после выплаты |
| S | |||
| 1 год | Sр | x | Sр – x |
| 2 год | (Sр – x)р = Sр2 – рx | x | Sр2 – xр – x |
| 3 год | р(Sр2 – xр – x) = Sр3 – хр2 – xр | x | - |
Sр3 – хр2 – xр = х
|
|
|
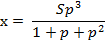
х = 1900800
2 равных платежа
| Год | Долг с % | Платеж | Долг после выплаты |
| S | |||
| 1 год | Sр | x | Sр – x |
| 2 год | (Sр – x)р = Sр2 – рx | x | - |
Sр2 – рx = х
Sр2 = рx + х
Sр2 = х(р + 1)
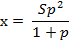
х = 2620800
За три года: 1900800 · 3 = 5702400
За два года: 2620800 · 2 = 5241600
Разница: 5702400 – 5241600 = 460800
Ответ: 460800 рублей.
Задача №3.
31 декабря 2014 года Алексей взял в банке 3689000 рублей в кредит под 12, 5% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12, 5%), затем Алексей переводит в банк платеж. Весь долг Алексей выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?
Решение:
Сумма кредита S = 3689000 рублей
Ставка r = 12, 5%, р = 1, 125
3 равных платежа
| Год | Долг с % | Платеж | Долг после выплаты |
| S | |||
| 1 год | Sр | x | Sр – x |
| 2 год | (Sр – x)р = Sр2 – рx | x | Sр2 – xр – x |
| 3 год | р(Sр2 – xр – x) = Sр3 – хр2 – xр | x | - |
Sр3 – хр2 – xр = х
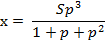
х = 1549125
2 равных платежа
| Год | Долг с % | Платеж | Долг после выплаты |
| S | |||
| 1 год | Sр | x | Sр – x |
| 2 год | (Sр – x)р = Sр2 – рx | x | - |
Sр2 – рx = х
Sр2 = рx + х
Sр2 = х(р + 1)
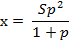
х = 2197125
За три года: 1549125 · 3 = 4647375
За два года: 2197125 · 2 = 4394250
Разница: 4647375 – 4394250 = 253125
Ответ: 253125 рублей.
6 тип: Задачи, связанные с известным остатком. (Фиксированные платежи)
Задача №1.
15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.
| Дата | 15. 01 | 15. 02 | 15. 03 | 15. 04 | 15. 05 | 15. 06 | 15. 07 |
| Долг (в процентах от кредита) | 100% | 90% | 80% | 70% | 60% | 50% | 0% |
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
|
|
|
Решение: S– сумма кредита
r = 5% - годовые (ежемесячные) проценты
р = 1+0, 01r – коэффициент (1, 05)
| Месяц | Долг с % | Платеж | Долг после выплаты |
| 15. 01 | S | ||
| 15. 02 | Sр | Sр – 0, 9S | 0, 9S |
| 15. 03 | 0, 9Sр | 0, 9Sр - 0, 8S | 0, 8S |
| 15. 04 | 0, 8Sр | 0, 8Sр - 0, 7S | 0, 7S |
| 15. 05 | 0, 7Sр | 0, 7Sр - 0, 6S | 0, 6S |
| 15. 06 | 0, 6Sр | 0, 6Sр - 0, 5S | 0, 5S |
| 15. 07 | 0, 5Sр | 0, 5Sр |
Общая сумма выплат:
(Sр + 0, 9Sр + 0, 8Sр + 0, 7Sр + 0, 6Sр + 0, 5Sр) – (0, 9S + 0, 8S + 0, 7S + 0, 6S + 0, 5S) = 4, 5Sр – 3, 5S = S(4, 5р – 3, 5)=S(4, 5 · 1, 05 – 3, 5)=1, 225S
Ответ: 22, 5 процента.
Задача №2.
15-го января планируется взять кредит в банке на 1 млн. рублей на 6 месяцев. Условия его возврата таковы:
− 1-го числа каждого месяца долг возрастает на целое число r процентов по сравнению с концом предыдущего месяца;
− со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
− 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей
| Долг | 15. 01 | 15. 02 | 15. 03 | 15. 04 | 15. 05 | 15. 06 | 15. 07 |
| Долг (в млн руб) | 0, 6 | 0, 4 | 0, 3 | 0, 2 | 0, 1 |
Найдите наибольшее значение r, при котором общая сумма выплат будет составлять менее 1, 2 млн рублей.
Решение:
Сумма кредита S = 1000000 рублей
r% - годовые (ежемесячные) проценты
р = 1 + 0, 01r
Найти: r%
| Месяц | Долг с % | Платеж | Долг после выплаты |
| 15. 01 | S | ||
| 15. 02 | Sр | Sр – 0, 6S | 0, 6S |
| 15. 03 | 0, 6Sр | 0, 6Sр - 0, 4S | 0, 4S |
| 15. 04 | 0, 4Sр | 0, 4Sр - 0, 3S | 0, 3S |
| 15. 05 | 0, 3Sр | 0, 3Sр - 0, 2S | 0, 2S |
| 15. 06 | 0, 2Sр | 0, 2Sр - 0, 1S | 0, 1S |
| 15. 07 | 0, 1Sр | 0, 1Sр |
Общая сумма выплат:
(Sр + 0, 6Sр + 0, 4Sр + 0, 3Sр + 0, 2Sр + 0, 1Sр) – (0, 6S + 0, 4S + 0, 3S + 0, 2S + 0, 1S) = 2, 6Sр – 1, 6S = S(2, 6р – 1, 6) = 1 · (2, 6р – 1, 6) = 2, 6р – 1, 6
2, 6р – 1, 6 < 1, 2
2, 6р < 2, 8
р < 1, 076
р = 1, 07
r = 7%
|
|
|


