 |
Ответ: 7. Ответ: 200 тысяч. 7 тип: Задачи, связанные с дифференцированными платежами. − с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
|
|
|
|
Ответ: 7
Задача №3.
В июле 2016 года планируется взять кредит в банке в размере S тыс. рублей, где S - натуральное число, на 3 года. Условия его возврата таковы:
− каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
− в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2016 | Июль 2017 | Июль 2018 | Июль 2019 |
| Долг (в тыс. рублей) | S | 0, 7S | 0, 4S |
Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.
Решение:
S– сумма кредита
r% - годовые (ежемесячные) проценты, r = 15%
р = 1+0, 01r, р = 1, 15
| Год | Долг с % | Платеж | Долг после выплаты |
| S | |||
| Sр | Sр – 0, 7S | 0, 7S | |
| 0, 7Sр | 0, 7Sр - 0, 4S | 0, 4S | |
| 0, 4Sр | 0, 4Sр |
1 выплата: 1, 15S – 0, 7S = 0, 45S = 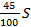 =
= 
2 выплата: 0, 7 · 1, 15S – 0, 4S = 0, 805S – 0, 4S = 0, 405S =  =
= 
3 выплата: 0, 4 · 1, 15S = 0, 46S =  =
= 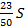
По условию, все выплаты должны быть целыми. Значит, число S должно делиться на 20, 200 и 50. Наименьшее общее кратное этих чисел равно 200.
Ответ: 200 тысяч.
7 тип: Задачи, связанные с дифференцированными платежами.
Задача №1.
Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r% этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r.
|
|
|
Решение:
S – cумма кредита,
р = 1+0, 01r
r -?
| Месяц | Долг с % | Выплата | Долг после выплаты |
| S | |||
| Sp | Sp – 
| 
| |

|  – – 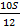
| 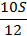
| |
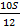 p p
| 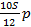 – – 
| 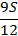
| |
 p p
|  – – 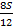
| 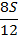
| |
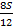 p p
|  – – 
| 
| |
 p p
| 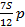 – – 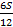
| 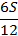
| |
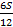 p p
|  – – 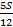
| 
| |
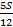 p p
| 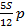 – – 
| 
| |
 p p
|  – – 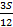
| 
| |
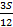 p p
|  – – 
| 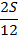
| |
 p p
| 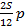 – – 
| 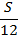
| |
 p p
| 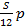
|
Sp(1 +  +
+ 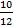 +
+  +
+  +
+  +
+  +
+ 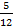 +
+  +
+ 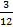 +
+  +
+ 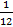 ) – S(
) – S(  +
+ 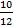 +
+  +
+  +
+  +
+  +
+ 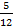 +
+  +
+ 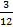 +
+  +
+ 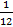 ) = 1, 13S
) = 1, 13S
 Sp –
Sp –  S = 1, 13S /: S
S = 1, 13S /: S
 p –
p –  = 1, 13/ · 12
= 1, 13/ · 12
78p – 66 = 13, 56
78p = 13, 56 + 66/: 78
р = 1, 02
r = 2%
Ответ: 2
Задача 2.
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
− 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
− со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
− 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что на пятый месяц кредитования нужно выплатить 57, 5 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Решение:
S – сумма кредита,
р = 1, 03
r = 3%
n = 9
Сумма всех выплат –?
| Месяц | Долг с % | Выплата | Долг после выплаты |
| S | |||
| Sp | Sp – 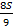
| 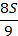
| |
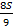 р р
| 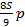 – – 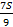
| 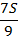
| |
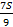 p p
| 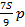 – – 
| 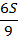
| |
 p p
|  – – 
| 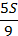
| |
 p p
|  – – 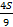
| 
| |
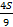 p p
|  – – 
| 
| |
 p p
|  – – 
| 
| |
 p p
| 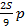 – – 
| 
| |
 p p
|  р р
|
 –
– 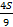 = 57, 5/ · 9
= 57, 5/ · 9
5Sр – 4S = 517, 5
S(5р – 4) = 517, 5
S(5 · 1, 03 – 4) = 517, 5
S = 450
Sp(1 +  +
+  +
+  +
+  +
+  +
+  +
+  +
+  ) – S(
) – S(  +
+  +
+  +
+  +
+  +
+  +
+  +
+  ) = 5Sр – 4S = S (5р – 4) = 450(5 · 1, 03 – 4) = 450 · 1, 15 = 517, 5
) = 5Sр – 4S = S (5р – 4) = 450(5 · 1, 03 – 4) = 450 · 1, 15 = 517, 5
Ответ: 517, 5 тысяч.
Задача 3.
15-го января планируется взять кредит в банке на несколько месяцев. Условия его возврата таковы:
− 1-го числа каждого месяца долг возврастает на 5% по сравнению с концом предыдущего месяца;
|
|
|
− со 2-го по 14-е число месяца необходимо выплатить часть долга;
− 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев можно взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит? (решение с помощью формулы суммы арифметической прогрессии)
Решение:
S – сумма кредита,
ставкаr = 5 %,
р = 1, 05
n=?
| Месяц | Долг с % | Выплата | Долг после выплаты |
| S | |||
| Sp | Sp – 
| 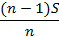
| |
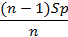
| 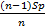 - - 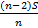
| 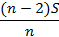
| |
| … | |||
| n – 1 | 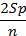
| 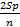 - - 
| 
|
| n | 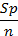
| 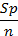
|
(Sp + 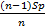 + … +
+ … + 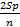 +
+ 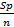 ) – (
) – (  -
- 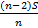 - … -
- … -  ) = 1, 25S
) = 1, 25S
Sp (1 +  + …+
+ …+  +
+  ) – S (
) – S (  -
- 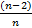 - … -
- … -  ) = 1, 25S
) = 1, 25S
По формуле суммы арифметической прогрессии получаем
Sp ·  – S ·
– S ·  = 1, 25S /: S
= 1, 25S /: S
p ·  –
–  = 1, 25 / · 2
= 1, 25 / · 2
1, 05 · (n + 1) – (n – 1) = 2, 5
1, 05n + 1, 05 – n + 1 = 2, 5
0, 05n = 0, 45
n = 9
Ответ: 9 месяцев.
8 тип: Нестандартные задачи, связанные с кредитом.
Задача 1.
В июле 2016 года планируется взять кредит в размере 6, 6 млн. руб. Условия возврата таковы:
− каждый январь долг возрастает на r% по сравнению с концом предыдущего года.
− с февраля по июнь необходимо выплатить часть долга.
− в июле 2017, 2018 и 2019 годов долг остается равным 6, 6 млн. руб.
− суммы выплат 2020 и 2021 годов равны.
Найдите r, если в 2021 году долг будет выплачен полностью и общие выплаты составят 12, 6 млн. рублей.
Решение:
S = 6, 6 млн. руб.
р = 1 + 0, 01r
r% =?
| Год | Долг с % | Выплата | Долг после выплаты |
| S | |||
| Sр | Sр – S | S | |
| Sр | Sр – S | S | |
| Sр | Sр – S | S | |
| Sр | x | Sр – х | |
| (Sр – x)р = Sр2 – xр | x |
1) Sр2 – xр = x
2) 3(Sр – S) + 2x = 12, 6
19, 8р – 19, 8 + 2x = 12, 6
х = 16, 2 – 9, 9р
1) 6, 6 р2 – (16, 2 – 9, 9р)р = 16, 2 – 9, 9р
6, 6 р2 – 16, 2р + 9, 9 р2 = 16, 2 – 9, 9р
16, 5 р2 – 6, 3р – 16, 2 = 0
165 р2 – 63р – 162 = 0
D=632+4•162•165=110889
b1=1, 2
b2= -0, 81не подходит по условию задачи.
Ответ: r=20.
Задача №2.
1 марта 2010 года Аркадий взял в банке кредит под 10% годовых. Схема выплаты кредита следующая: 1 марта каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Аркадий переводит в банк платеж. Весь долг Аркадий выплатил за 3 платежа, причем второй платеж оказался в два раза больше первого, а третий – в три раза больше первого. Сколько рублей взял в кредит Аркадий, если за три года он выплатил банку 2 395 800 рублей?
|
|
|
Решение:
Сумма кредита (S)-?
Ставка (а)=10%, b=1, 1
Количество лет (n) 3 года
| Год | Долг с % | Выплата | Долг после выплаты | |
| S | ||||
| Sb | x | Sb-x | ||
| (Sb-x)b=Sb2-xb | 2x | Sb2-xb-2x | ||
| (Sb2-xb-2x)b=Sb3-xb2-2xb | 3х | Полная выплата - | ||
| остаток 0 | ||||
| x+2x+3x=2395800 | ||||
| 6x=2395800 | ||||
| x=399300 | ||||
Sb3_ хb2-2xb =3x
Sb3-(3+2b+b2)x=0
| S= | (3 2b b2 )x | | 399300 (3 2, 2 1, 21) | | 399300 6, 41 | 1923000 рублей | |
| b3 | 1, 331 | 1, 331 | |||||
|
|
|


