 |
Сборник задач по дискретной математике
|
|
|
|
Глазовский инженерно-экономический институт
(филиал ИжГТУ)
Сборник задач
по дискретной математике
Глазов 2005
Сборник задач по дискретной математике
(методическое пособие)
Составитель: канд. пед. наук, доцент кафедры ЭНиГД Щепин О. Н.
Методическое пособие предназначено для студентов очного и заочного отделения ГИЭИ, обучающихся по специальности 220200: Автоматизированные системы обработки информации и управления.
© ГИЭИ, 2005
Оглавление
| Предисловие | |
| 1. Множества. Операции над множествами | |
| 2. Бинарные отношения | |
| 3. Способы задания булевых функций | |
| 4. Функции алгебры логики | |
| 5. Совершенные формы и разложение Шеннона | |
| 6. Минимизация булевых функций | |
| 7. Многочлены Жегалкина | |
| 8. Основные классы булевых функций | |
| 9. Полные системы булевых функций | |
| 10. Схемы из функциональных элементов и контактно релейные схемы | |
| 11. Частичные булевы функции | |
| 12. Различные способы задания графов. Операции над графами | |
| 13. Минимальные деревья | |
| 14. Гамильтоновы графы | |
| 15. Кратчайшие пути на графе | |
| 16. Эйлеровы графы |
Предисловие
Пособие предназначено для студентов младших курсов ГИЭИ (филиал ИжГТУ) обучающихся по специальности 220200: Автоматизированные системы обработки информации и управления. В пособии содержится 16 тем семинарских занятий по трем основным разделам дискретной математики: " Теория множеств и отношений", " Булевы функции" и " Теория графов". Каждая тема содержит: минимальные теоретические сведения, примеры решений типовых задач, серию задач для самостоятельного решения.
|
|
|
Тема 1. Множества. Операции над множествами
Краткая теория
 – универсальное множество (универсум);
– универсальное множество (универсум);
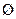 – пустое множество;
– пустое множество;
 (подмножества универсума);
(подмножества универсума);
 – задание множества перечислением;
– задание множества перечислением;
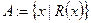 – задание множества характеристическим предикатом
– задание множества характеристическим предикатом  (характеристическим свойством);
(характеристическим свойством);
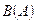 – булеан множества
– булеан множества 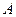 (множество всех подмножеств множества
(множество всех подмножеств множества 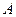 );
);
 – объединение множеств
– объединение множеств 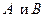 ;
;
 – пересечение множеств
– пересечение множеств 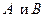 ;
;
 – разность множеств
– разность множеств 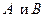 ;
;
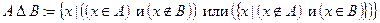 – симметрическая разность множеств
– симметрическая разность множеств 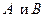 ;
;
 – дополнение множества;
– дополнение множества;
 – равенство множеств;
– равенство множеств;
 – признак равенства множеств.
– признак равенства множеств.
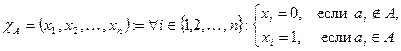 – характеристический вектор множества
– характеристический вектор множества 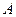 (
(  ).
).
Примеры решения задач
Задача 1. Найти с помощью диаграмм Эйлера-Венна  , если
, если 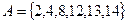 и
и  .
.
Решение:

Ответ: 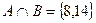 .
.
Задача 2. Найти по определению  , если
, если  ,
,  ,
, 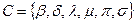 .
.
Решение:
 ,
,
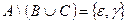 .
.
Ответ: 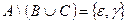 .
.
Задача 3. Используя характеристические вектора найти  , если
, если 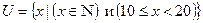 ,
, 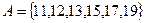 ,
, 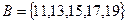 ,
,  .
.
Решение:
 ,
, 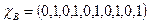 ,
, 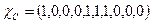 .
.
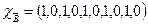 ,
,
 ,
,
 .
.
Ответ: 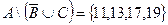 .
.
Задача 4. Проверить справедливость равенства: 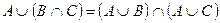 .
.
Решение:
Первый способ (с помощью диаграмм Эйлера-Венна)

Так как соответствующие диаграммы Эйлера-Венна получились одинаковыми, то равенство выполняется.
Второй способ
Для доказательства равенства воспользуемся признаком равенства множеств.
Пусть 
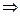

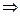
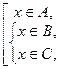
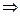

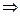

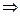
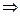
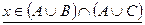 .
.
Пусть 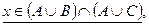
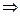

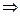

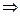
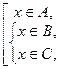
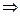
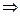

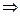
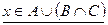 .
.
Таким образом, по признаку равенства множеств, имеем 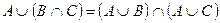 .
.
Упражнения
1. 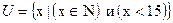 ,
, 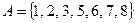 ,
,  ,
,  .
.
a) Найти с помощью диаграмм Эйлера-Венна: 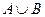 ,
,  ,
, 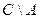 ,
, 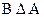 ,
, 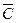 ;
;
b) Найти по определению и с помощью использования характеристических векторов: 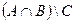 ,
, 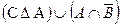 .
.
2. 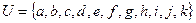 ,
,  ,
, 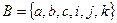 ,
,  .
.
a) Найти с помощью диаграмм Эйлера-Венна: 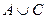 ,
, 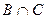 ,
, 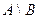 ,
, 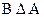 ,
,  ;
;
b) Найти по определению и с помощью использования характеристических векторов:  ,
, 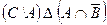 .
.
3. Проверить справедливость равенств:
a) 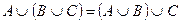 ;
;
b)  ;
;
c)  ;
;
d)  ;
;
e)  ;
;
f) 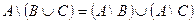 ;
;
g)  ;
;
h) 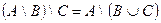 ;
;
i)  ;
;
j)  ;
;
k) 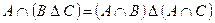 ;
;
l)  .
.
Дополнительные упражнения
|
|
|
4. Проверить справедливость выражений:
a)  ;
;
b) 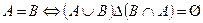 ;
;
c)  и
и  ;
;
d)  и
и 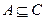 .
.
5.  . Решить систему уравнений:
. Решить систему уравнений:
a) 
b) 
Тема 2. Бинарные отношения
Краткая теория
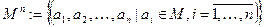 – n-ая декартова степень множества M.
– n-ая декартова степень множества M.
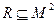 – бинарное отношение, заданное над множеством М.
– бинарное отношение, заданное над множеством М.
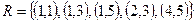 – задание отношения перечислением.
– задание отношения перечислением.

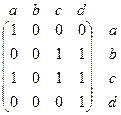 – задание отношения матрицей смежности.
– задание отношения матрицей смежности.

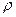 – свойство рефлексивности. Отношение R обладает свойством
– свойство рефлексивности. Отношение R обладает свойством 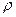 , если
, если  .
.
 – свойство антирефлексивности. Отношение R обладает свойством
– свойство антирефлексивности. Отношение R обладает свойством  , если
, если  .
.
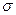 – свойство симметричности. Отношение R обладает свойством
– свойство симметричности. Отношение R обладает свойством 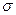 , если
, если  .
.
 – свойство антисимметричности. Отношение R обладает свойством
– свойство антисимметричности. Отношение R обладает свойством  , если
, если  .
.
 – свойство транзитивности. Отношение R обладает свойством
– свойство транзитивности. Отношение R обладает свойством  , если
, если 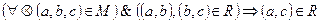 .
.
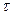 – свойство толерантности. Отношение R обладает свойством
– свойство толерантности. Отношение R обладает свойством 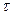 , если R обладает свойствами
, если R обладает свойствами 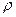 и
и 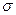 .
.
~ – свойство эквивалентности. Отношение R обладает свойством ~, если R обладает свойствами 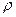 ,
, 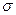 и
и  .
.
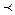 - отношение предпорядка. Отношение R обладает свойством
- отношение предпорядка. Отношение R обладает свойством 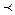 , если R обладает свойствами
, если R обладает свойствами 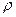 и
и  .
.
 - отношение нестрогого порядка. Отношение R обладает свойством
- отношение нестрогого порядка. Отношение R обладает свойством  , если R обладает свойствами
, если R обладает свойствами 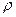 ,
,  и
и  .
.
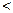 - отношение порядка (строгого порядка). Отношение R обладает свойством
- отношение порядка (строгого порядка). Отношение R обладает свойством 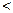 , если R обладает свойствами
, если R обладает свойствами  ,
,  и
и  .
.
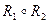 : =
: =  – композиция отношений
– композиция отношений 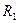 и
и 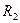 .
.
|
|
|


