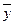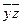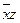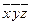|
Примеры решения задач. Упражнения. Дополнительные упражнения. Тема 6. Минимизация булевых функций. Краткая теория. a) Для удобства равносильные преобразования будем производить в строку
|
|
|
|
Примеры решения задач
Задача. Найти совершенные формы для формул с помощью равносильных преобразований и с помощью разложения Шеннона:
a)  ;
;
b) 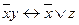 .
.
Решение:
a) Для удобства равносильные преобразования будем производить в строку.



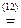
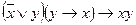
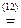
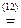

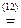


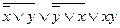


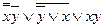


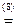

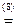
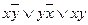 (ДНФ, СДНФ).
(ДНФ, СДНФ).
Найдем КНФ:
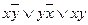


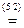






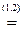
 (КНФ, СКНФ).
(КНФ, СКНФ).
Разложение Шеннона:

| 
| 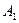
| 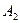
| 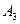
| |

| |||||

| |||||

| |||||

|
 ;
;
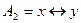 ;
;
 .
.
СДНФ:  .
.
СКНФ:  .
.
b) Все преобразования по одно и той же равносильности будем производить одновременно.
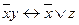

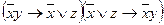
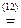



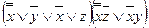
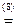



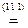
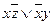 (ДНФ).
(ДНФ).
Найдем СДНФ, внедрив недостающие переменные, удалим повторяющиеся ЭК и упорядочим лексикографически:
 =
= 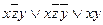 =
=  =
=  (СДНФ).
(СДНФ).
Найдем КНФ:
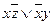

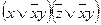

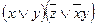

 (КНФ).
(КНФ).
Найдем аналогично СКНФ:
 =
= 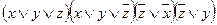 =
=
=  =
=
= 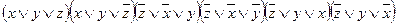 =
=
=  (СКНФ).
(СКНФ).

| 
| 
| 
| 
| 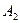
| 
| |
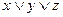
| |||||||
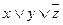
| |||||||

| |||||||
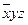
| |||||||

| |||||||
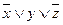
| |||||||

| |||||||
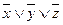
|
Разложение Шеннона:
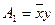 ;
;
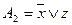 ;
;
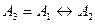 .
.
СДНФ:  .
.
СКНФ: 
 .
.
Упражнения
1. С помощью равносильных преобразований найти нормальные формы для формул:
a) 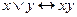 ;
;
b)  ;
;
c)  ;
;
d)  ;
;
e)  .
.
2. Найти совершенные формы методом равносильных преобразований и проверить результат методом разложения Шеннона для формул:
a) 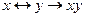 ;
;
b) 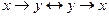 ;
;
c) 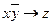 ;
;
d)  ;
;
e) 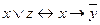
f) 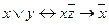 ;
;
g) 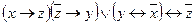 ;
;
h) 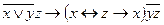 .
.
Дополнительные упражнения
3. Выполнить разложение Шеннона по переменной х для функций заданных формулами:
a) 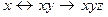 ;
;
b)  .
.
Тема 6. Минимизация булевых функций
Краткая теория
Будем рассматривать минимизацию булевых функций только в форме ДНФ, т. е. будем искать минимальную ДНФ (МДНФ).
Процесс отыскания МДНФ из СДНФ представляет собой три этапа:
|
|
|
1. Нахождение сокращенной ДНФ;
2. Нахождение тупиковых ДНФ;
3. Выбор среди тупиковых ДНФ минимальной.
ДНФ называется сокращенной, если она получена из СДНФ с помощью операций склейки и поглощения, примененных столько раз, сколько это возможно.
Операция склейки: 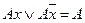 .
.
Операция поглощения:  .
.
ДНФ называется тупиковой, если при отбрасывании любой ее ЭК мы получаем не равносильную ей формулу. Таким образом процесс нахождения тупиковых ДНФ заключается в полном переборе комбинаций ЭК сокращенной ДНФ. Очевидно, что таких комбинаций может быть несколько, МДНФ находится среди них.
Для облегчения поиска тупиковых ДНФ необходимо среди всего множества ЭК выбрать базисные, которые входят в ядро ДНФ. Это те ЭК которые входят во все тупиковые ДНФ. В общем случае их может и не быть.
Примеры решения задач
Задача. Найти МДНФ графическим методом, методом Квайна и методом карт Карно для булевой функции заданной десятичным кодом  .
.
Решение: Найдем сначала СДНФ с помощью разложения Шеннона.
| x | y | z | 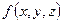
| |

| ||||
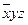
| ||||

| ||||

| ||||
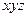
|
СДНФ: 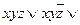
 .
.
Графический метод
Перепишем СДНФ в виде: 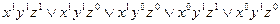 , где
, где
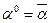 ,
,  .
.
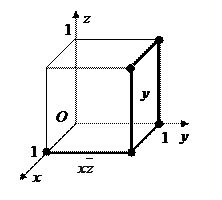 Упорядоченные тройки 0 и 1 будем рассматривать как координаты точек трехмерного пространства. В итоге мы получили следующие координаты: (1, 1, 1), (1, 1, 0), (1, 0, 0), (0, 1, 1), (0, 1, 0).
Упорядоченные тройки 0 и 1 будем рассматривать как координаты точек трехмерного пространства. В итоге мы получили следующие координаты: (1, 1, 1), (1, 1, 0), (1, 0, 0), (0, 1, 1), (0, 1, 0).
Очевидно, что все они являются некоторыми координатами куба с ребром равным единице, который помещен в начало координат. Выделим полученные вершины. Если две смежные вершины куба выделены, то выделяем все ребро. Если все ребра грани выделены, то выделяем всю грань. Каждой вершине соответствует ЭК длины три, каждому ребру – длины два, каждой грани – длины один. Очевидно, что двум выделенным точкам (1, 0, 0) и (1, 1, 0) соответствует выделенное ребро ЭК которого равна 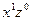 (
( 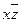 ). А выделенной грани – y.
). А выделенной грани – y.
|
|
|
| ЭК | 1я склейка | 2я склейка | |
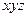
|  (1, 2) (1, 2)
|  (1, 2, 4, 5) (1, 2, 4, 5)
| |

|  (1, 4) (1, 4)
|  (1, 4, 2, 5) (1, 4, 2, 5)
| |

| 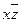 (2, 3) (2, 3)
| ||
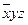
| 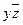 (2, 5) (2, 5)
| ||

|  (4, 5) (4, 5)
|
Для получения тупиковой ДНФ необходимо рассмотреть покрытия выделенных вершин выделенными элементами. Очевидно, что такое покрытие состоит из одного ребра и одной грани. Таким образом, Тупиковой ДНФ будет 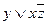 . Она же и является МДНФ.
. Она же и является МДНФ.
Метод Квайна
| ЭК | 1я склейка | 2я склейка | |
 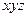
|   (1, 2) (1, 2)
|  (1, 2, 4, 5) (1, 2, 4, 5)
| |
| 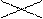  (1, 4) (1, 4)
|   (1, 4, 2, 5) (1, 4, 2, 5)
| |
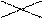 
| 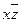 (2, 3) (2, 3)
| ||
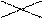 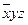
|  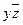 (2, 5) (2, 5)
| ||
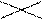 
|   (4, 5) (4, 5)
|
Выпишем все ЭК в первый столбец таблицы. Во второй столбец запишем все возможные склейки элементов первого столбца (в скобочках указаны номера склеиваемых ЭК). Процесс склейки продолжается до тех пор, пока это возможно. Результат второй склейки  покрывает 1, 2, 4 и 5 ЭК, для покрытия оставшейся 3 ЭК используем
покрывает 1, 2, 4 и 5 ЭК, для покрытия оставшейся 3 ЭК используем 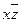 .
.
Учитывая закон идемпотентности дизъюнкции получим МДНФ: 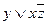 .
.
Метод карт Карно
Отметим в таблице строки содержащие ЭК СДНФ. Остальные строки вычеркнем.
|
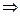
|
|
Вычеркнем все элементы столбцов равные выражениям в вычеркнутых строках, после чего применим законы поглощения.
|
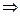
|
|
Необходимо найти покрытие непустых строк столбцами, причем с учетом того, что ячейки таблицы с одинаковым содержанием рассматриваются одновременно.
Таким образом, МДНФ: 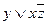 .
.
|
|
|