 |
Упражнения. Дополнительные упражнения. Тема 7. Многочлены Жегалкина. Краткая теория. Примеры решения задач. 2. Минимизировать методом Квайна и методом карт Карно булевы функции:
|
|
|
|
Упражнения
1. Минимизировать графическим методом, методом Квайна и методом карт Карно булевы функции:
a) 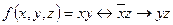 ;
;
b)  ;
;
c)  ;
;
d)  ;
;
e) 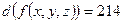 .
.
2. Минимизировать методом Квайна и методом карт Карно булевы функции:
a)  ;
;
b)  ;
;
c)  ;
;
d) 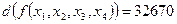 ;
;
Дополнительные упражнения
3. Минимизировать булевы функции, используя гиперкуб:
a) 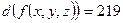 ;
;
b) 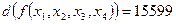 .
.
Тема 7. Многочлены Жегалкина
Краткая теория

| 
| 
|
Многочленом Жегалкина называется формула, содержащая только операции конъюнкции над переменными, сложения по модулю два над ЭК (Å ) и константу 1.
Примеры: 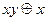 ;
;  .
.
Любая булева функция однозначно представима многочленом Жегалкина. При этом представление булевой функции в виде многочлена Жегалкина позволяет также находить фиктивные переменные функции.
Примеры решения задач
| x | y | z | 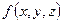
|
Задача. Найти разложение функции  в полином Жегалкина и выяснить содержит ли она фиктивные переменные.
в полином Жегалкина и выяснить содержит ли она фиктивные переменные.
Решение:
Будем искать разложение в виде:
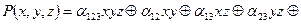

где  методом неопределенных коэффициентов.
методом неопределенных коэффициентов.
Для этого будем подставлять в многочлен различные наборы переменных так, чтобы ровно один  на этом наборе не обращался в ноль (с учетом уже найденных
на этом наборе не обращался в ноль (с учетом уже найденных  ).
).
| x | y | z | 
| 
| x | y | z | 
| 
| |
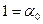
| 
| 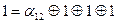
| 
| |||||||

| 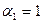
| 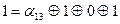
| 
| |||||||
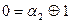
| 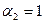
| 
| 
| |||||||
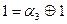
| 
| 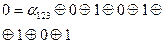
| 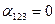
|
Таким образом
 .
.
Т. к. в разложении функции в полином Жегалкина учувствуют все переменные, то фиктивных переменных нет.
Упражнения
1. Найти полином Жегалкина и выяснить содержит ли функция фиктивные переменные:
|
|
|
a) 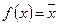 ;
;
b)  ;
;
c) 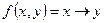 ;
;
d)  ;
;
e) 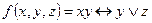 ;
;
f)  ;
;
g) 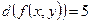 ;
;
h) 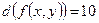 ;
;
i) 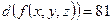 ;
;
j)  ;
;
k)  .
.
Дополнительные упражнения
2. Найти полином Жегалкина для функции:
a)  ;
;
b)  .
.
Тема 8. Основные классы булевых функций
Краткая теория
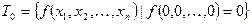 – класс функций сохраняющих 0.
– класс функций сохраняющих 0.
 – класс функций сохраняющих 1.
– класс функций сохраняющих 1.
 – класс самодвойственных функций.
– класс самодвойственных функций.
 – класс монотонных функций.
– класс монотонных функций.
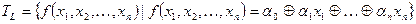 – класс линейных функций.
– класс линейных функций.
Функция 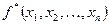 двойственна функции
двойственна функции 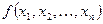 , если
, если  .
.
Замыканием класса K булевых функций (обозначается [K]) называется множество всех функций, которые можно реализовать с помощью формул функций данного класса.
Определение формулы над данным классом функций:
1. Любая функция класса является формулой;
2. Если 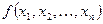 функция данного класса, а
функция данного класса, а 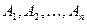 формулы, то формулой будет
формулы, то формулой будет 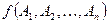 ;
;
3. Других формул нет.
Примеры решения задач
Задача 1. Доказать замкнутость класса  .
.
Решение: Доказательство проведем методом математической индукции по определению формулы.
База индукции: Очевидно, что 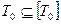 , т. е. любая функция, сохраняющая 0, принадлежит своему замыканию.
, т. е. любая функция, сохраняющая 0, принадлежит своему замыканию.
Индуктивное предположение: Пусть все формулы, полученные не более чем за k шагов, сохраняют 0.
Индуктивный переход: Докажем, что и формула, полученная за k+1 шаг, сохраняет 0. По определению формулы функция  , реализуемая формулой, должна иметь вид:
, реализуемая формулой, должна иметь вид:  =
= 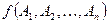 , где
, где 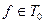 , а
, а 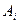 – формулы сохраняющие 0 по индуктивному предположению. Тогда
– формулы сохраняющие 0 по индуктивному предположению. Тогда
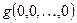 =
=  =
= 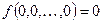 и
и  .
.
Индукция доказана полностью и  .
.
Задача 2. Найти функцию двойственную для функции  .
.
Решение:
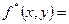
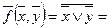
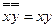 .
.
Задача 3. Выяснить каким классам принадлежит функция  .
.
Решение:
1. 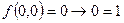 Þ
Þ  .
.
2.  Þ
Þ  .
.
3. 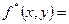

 . Т. к.
. Т. к. 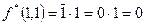 , а
, а  , то
, то  и
и  .
.
4. 
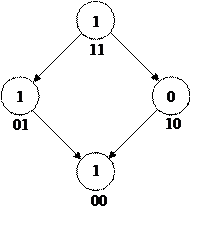 Для доказательства монотонности воспользуемся гиперкубом.
Для доказательства монотонности воспользуемся гиперкубом.
Для того, чтобы выполнялась монотонность необходимо и достаточно, чтобы ни один 0 не покрывался бы 1. Для нашей функции это не выполняется:
 . Таким образом
. Таким образом 
|
|
|
5. Для доказательства линейности применим метод неопределенных коэффициентов.
 .
.
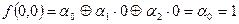 .
.
 Þ
Þ 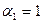 .
.
 Þ
Þ  .
.
Если существует разложение, то оно имеет вид  , проверим его справедливость на последнем наборе.
, проверим его справедливость на последнем наборе.
 , но
, но 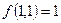 . Противоречие. Значит такого разложения нет и
. Противоречие. Значит такого разложения нет и  .
.
|
|
|


