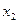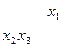|
Примеры решения задач. Упражнения. Дополнительные упражнения. Тема 3. Способы задания булевых функций. Краткая теория. Первый способ (по определению)
|
|
|
|
Примеры решения задач
Задача 1.  .
.  .
.
 . Найти:
. Найти:
a) 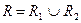 и выяснить какими свойствами оно обладает;
и выяснить какими свойствами оно обладает;
b)  .
.
Решение:
а)  .
.
Первый способ (по определению)
Т. к. 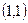 ,
, 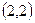 ,
, 
 , то
, то  рефлексивно (
рефлексивно ( 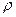 ) и не обладает свойством антирефлексивности (
) и не обладает свойством антирефлексивности (  ).
).
Т. к.  и
и 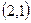 ,
,  и
и 
 , а других пар с различными элементами нет, то
, а других пар с различными элементами нет, то  обладает свойством симметричности (
обладает свойством симметричности ( 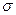 ) и не обладает свойством антисимметричности (.
) и не обладает свойством антисимметричности (.  ).
).
Т. к.  ,
, 
 , а
, а 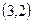
 , то
, то  не обладает свойством транзитивности (
не обладает свойством транзитивности (  ).
).
Таким образом,  есть отношение толерантности (
есть отношение толерантности ( 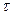 ) и не является ни отношением эквивалентности ( ~ ), ни отношениями порядка (
) и не является ни отношением эквивалентности ( ~ ), ни отношениями порядка ( 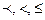 ).
).
Второй способ (графический)
 Т. к. для каждой вершины есть петля, то
Т. к. для каждой вершины есть петля, то  рефлексивно.
рефлексивно.
Т. к. для вершины 1 есть петля, то  не антирефлексивно.
не антирефлексивно.
Т. к. каждая дуга имеет обратную, то  симметрично.
симметрично.
Т. к. для дуги  есть дуга
есть дуга 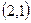 , то
, то  не антисимметрично.
не антисимметрично.
Т. к. две последовательные дуги  и
и  не имеют замыкания (дуги
не имеют замыкания (дуги 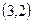 ), то
), то  не транзитивно.
не транзитивно.
Остальное как в первом случае.
Третий способ (матричный)
 Т. к. по главной диагонали стоят все единицы, то то
Т. к. по главной диагонали стоят все единицы, то то  рефлексивно, но не антирефлексивно.
рефлексивно, но не антирефлексивно.
Т. к. матрица симметрична относительно главной диагонали, то  симметрично, но не антисимметрично (существуют единицы вне главной диагонали).
симметрично, но не антисимметрично (существуют единицы вне главной диагонали).
Т. к.  ,
, 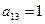 ,
,  , то
, то  не транзитивно.
не транзитивно.
Остальное как в первом случае.
b) Найдем композицию отношений используя граф Кёнига.


Таким образом 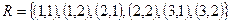 .
.
Задача 2. Отношения 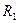 и
и 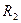 обладают свойством
обладают свойством 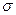 . Выясните, обладают ли свойством
. Выясните, обладают ли свойством 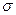 отношение
отношение  , если
, если 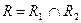 .
.
Решение:
МОП
Допустим, что  не обладает свойством
не обладает свойством 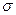 . Тогда найдется пара
. Тогда найдется пара 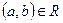 , такая что пара
, такая что пара  . Допустим для простоты, что она принадлежала
. Допустим для простоты, что она принадлежала 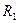 . Следовательно, в силу того, что
. Следовательно, в силу того, что 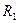 обладает свойством
обладает свойством 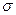 , и пара
, и пара  , и пара
, и пара  принадлежат
принадлежат 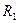 . Но из определения пересечения множеств следует, что пара
. Но из определения пересечения множеств следует, что пара  должна принадлежать
должна принадлежать 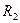 , а пара
, а пара  не должна, что противоречит тому, что
не должна, что противоречит тому, что 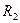 обладает свойством
обладает свойством 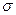 . Таким образом предположение неверно и
. Таким образом предположение неверно и  обладает свойством
обладает свойством 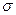 .
.
|
|
|
Упражнения
1. 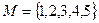 .
. 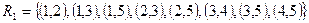 ,
,
 ,
,
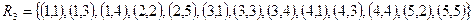 .
.
a) Построить соответствующие ориентированные графы, матрицы смежности, графы Кёнига и определить основные свойства отношений 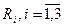 .
.
b) Найти: 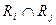 ,
,  ,
, 
 , где
, где  и
и  .
.
2. 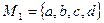 . Приведите примеры отношений обладающих свойствами:
. Приведите примеры отношений обладающих свойствами: 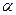 ,
,  ,
, 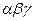 , где
, где  и
и  .
.
3. Отношения 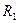 и
и 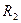 обладают свойством
обладают свойством 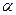 , где
, где  . Выясните, обладают ли свойством
. Выясните, обладают ли свойством 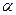 :
:
a) 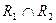 ;
;
b) 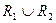 ;
;
c) 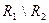 ;
;
d)  .
.
4.  .
.  ,
, 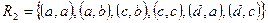 ,
,  .
.
Найти 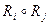 , если
, если  ,
, 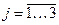 .
.
Дополнительные упражнения
5. Пусть  бинарное отношение, заданное на множестве
бинарное отношение, заданное на множестве  . Найти свойства отношений
. Найти свойства отношений  ,
,  ,
, 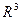 .
.
6. Пусть  бинарное отношение, заданное на множестве
бинарное отношение, заданное на множестве  . Построить график и найти свойства отношений
. Построить график и найти свойства отношений  ,
,  .
.
Тема 3. Способы задания булевых функций
Краткая теория
Булевыми функциями называются функции вида:  , где
, где 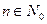 .
.
Другими словами булева функция ставит в соответствие n-ке нулей и единиц либо нуль, либо единицу:  . Всего всевозможных различных наборов которые могут принимать аргументы булевой функции
. Всего всевозможных различных наборов которые могут принимать аргументы булевой функции 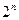 и значит любая булева функция может быть задана их перечислением и значением функции на каждом наборе. Для того, чтобы избежать потери наборов переменных используют лексикографический порядок их записи. Пример такой записи приведен ниже. Любой набор значений переменных можно рассматривать как число записанное в двоичной системе счисления. Лексикографический порядок в этом случае будет совпадать с записью чисел от 0 до
и значит любая булева функция может быть задана их перечислением и значением функции на каждом наборе. Для того, чтобы избежать потери наборов переменных используют лексикографический порядок их записи. Пример такой записи приведен ниже. Любой набор значений переменных можно рассматривать как число записанное в двоичной системе счисления. Лексикографический порядок в этом случае будет совпадать с записью чисел от 0 до 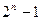 . Так для двух переменных (0, 0) – 0, (0, 1) – 1, (1, 0) – 2, (1, 1) – 3.
. Так для двух переменных (0, 0) – 0, (0, 1) – 1, (1, 0) – 2, (1, 1) – 3.
Примеры решения задач
Задача. Найти различные способы задания булевой функции 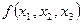 заданной одномерной таблицей:
заданной одномерной таблицей:
| Замечание
Одномерная таблица является компактной записью множества выражений вида:
 ; ;
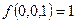 ; ;
 ;
… ;
…
 . .
|
Решение:
Найдем различные способы задания для 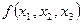 .
.
1. Двумерной таблицей:
| Аналогично строятся двумерные таблицы для четырех, пяти и более переменных, при этом переменные делятся на две группы  и и  , ,  и и  , и т. д. Допускается также и биение другое биение переменных на группы. Например: , и т. д. Допускается также и биение другое биение переменных на группы. Например:  и и  . Также, иногда меняют местами группы, т. е. первая группа записывается в столбец, а вторая в строку. . Также, иногда меняют местами группы, т. е. первая группа записывается в столбец, а вторая в строку.
|
2. Характеристическим вектором:
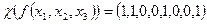 .
.
Он представляет собой транспонированный последний столбец одномерной таблицы.
3. Множеством номеров строк, на которых функция принимает значение единица (нумерация ведется путем перевода наборов значений переменных из двоичной системы в десятичную. Например 0102 = 210):
 .
.
4. Множеством номеров строк, на которых функция принимает значение нуль:
 .
.
5. Системой:
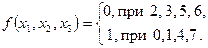
Система является объединением двух предыдущих способов и применяется при работе с частичными (не всюду определенными) функциями.
6. Десятичным кодом:
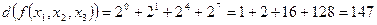 .
.
7. Аналитически (СДНФ):
 или
или  .
.
 Более подробно данный вид задания булевых функций, имеющий очень важное значение, будет рассматриваться в последующих темах.
Более подробно данный вид задания булевых функций, имеющий очень важное значение, будет рассматриваться в последующих темах.
8. Гиперкубом:
В каждой строке находятся вершины графа соответствующие наборам с одинаковым количеством единиц расположенных в алфавитном порядке. Стрелками соединяются вершины, соответствующие наборы которых отличаются ровно в одной позиции.
Данный вид задания булевой функции используется для доказательства монотонности булевых функций.
|
|
|