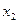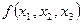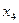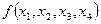|
Упражнения. Дополнительные упражнения. Тема 4. Функции алгебры логики. Краткая теория. Примеры решения задач. Рассмотреть два случая, когда a принимает значения 0 и 1.
|
|
|
|
Упражнения
1. Найти различные способы задания булевой функции заданной одномерной таблицей:
a)
| b)
|
Рассмотреть два случая, когда a принимает значения 0 и 1.
2. Найти различные способы задания булевой функции заданной десятичным кодом:
a)  ;
;
b) 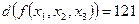 ;
;
c) 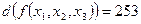 .
.
Замечание. В случае возникновения затруднений рекомендуется использование разложения десятичного числа в двоичное делением столбиком, либо с помощью калькулятора. Необходимо учесть то, что полученное число будет иметь обратную нумерацию разрядов:

Дополнительные упражнения
3. Найти различные способы задания булевой функции заданной одномерной таблицей:
|
|
4. Найти различные способы задания булевой функции заданной десятичным кодом: 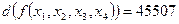 .
.
Тема 4. Функции алгебры логики
Краткая теория
Каждой логической операции над высказываниями взаимнооднозначно соответствует некоторая булева функция. Такие булевы функции традиционно называю логическими или функциями алгебры логики.
| Логическая связка | Логическая операция | Обозначения | Пример |
| " и" | конъюнкция | 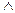 , ,  , × , ×
| 
|
| " или" | дизъюнкция |  , + , +
| 
|
| " если …, то …" | импликация | 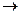 , , 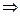
| 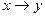
|
| " … тогда и только тогда, когда …" | эквиваленция | 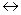 , , 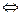
| 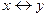
|
| " не …" | отрицание |  , , 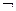
| 
|
|
|
|
|
|
Приоритет:  ,
,  ,
,  ,
, 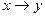 ,
, 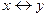 (слева на право).
(слева на право).
Договоренности:
· знак конъюнкции не писать;
· учитывая приоритет операций не писать лишние скобки включая внешние.
Основные равносильности алгебры логики:
| Законы идемпотентности | |
1. 1. 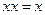
| 1. 2. 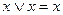
|
| Законы ассоциативности | |
2. 1. 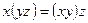
| 2. 2. 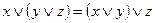
|
| Законы коммутативности | |
3. 1. 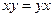
| 3. 2. 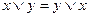
|
| Законы дистрибутивности | |
4. 1. 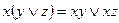
| 4. 2. 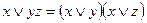
|
| Законы поглощения | |
5. 1. 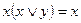
| 5. 2. 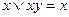
|
| Законы Порецкого | |
6. 1. 
| 6. 2. 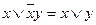
|
| Законы де Моргана | |
7. 1. 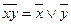
| 7. 2. 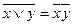
|
| Закон двойного отрицания | |
| 8. | |
| Закон исключенного третьего | |
9. 1. 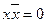
| 9. 2. 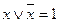
|
| Законы действий с константой 0 | |
10. 1. 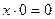
| 10. 2. 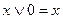
|
| Законы действий с константой 1 | |
11. 1. 
| 11. 2. 
|
| Представление импликации через отрицание и конъюнкцию | |
| 12. | |
| Представление эквиваленции через импликацию и конъюнкцию | |
| 13. | |
Примеры решения задач
Задача 1. Найти таблицу истинности для функции заданной формулой:
a)  ;
;
b) 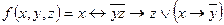 .
.
Решение:
a)  Разобьем формулу на подформулы, учитывая приоритет операций:
Разобьем формулу на подформулы, учитывая приоритет операций:

| 
| 
| 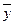
| 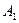
| 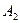
| 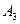
| 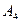
|
 ;
;
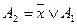 ;
;
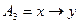 ;
;
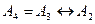 .
.
b) Разобьем формулу на подформулы, учитывая приоритет операций:
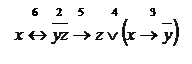

| 
| 
| 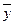
| 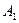
| 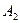
| 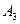
| 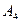
| 
| 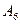
|
 ;
;
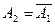 ;
;
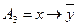 ;
;
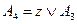 ;
;
 ;
;
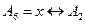 .
.
Задача 2. Проверить равносильность формул:
a) 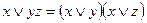 ;
;
b)  .
.
Решение:

| 
| 
| 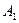
| 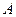
| 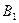
| 
| 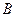
|
a) 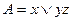 ;
; 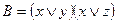 .
.
|
|
|
 ;
;
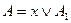 ;
;
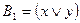 ;
;
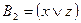 ;
;

Т. к. столбцы 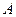 и
и 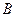 совпадают,
совпадают,
то формулы равносильны.

| 
| 
| 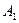
| 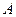
| 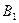
| 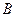
|
b) 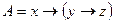 ;
; 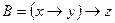 .
.
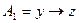 ;
;
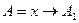 ;
;
 ;
;
 .
.
Т. к. столбцы 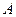 и
и 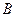 не совпадают,
не совпадают,
то формулы неравносильны.
Упражнения
1. Найти таблицы истинности для формул:
a)  ;
;
b) 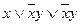 ;
;
c)  ;
;
d) 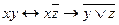 ;
;
e) 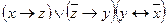 ;
;
f) 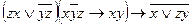 ;
;
g) 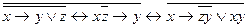 .
.
2. Доказать основные равносильности и равносильности для импликации и эквиваленции используя таблицы истинности.
3. Проверить равносильность формул:
a) 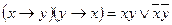 ;
;
b) 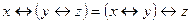 ;
;
c) 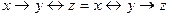 ;
;
d)  .
.
Дополнительные упражнения
4. Найти таблицы истинности для формул:
a) 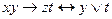 ;
;
b) 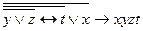 .
.
Тема 4. Совершенные формы и разложение Шеннона
Краткая теория
Переменную или ее отрицание будем называть литералом.
Формула, представляющая собой конъюнкцию (дизъюнкцию) литералов, называется элементарной конъюнкцией (дизъюнкцией) [ЭК (ЭД)].
Конъюнктивной (дизъюнктивной) нормальной формой [КНФ (ДНФ)] называется формула, представляющая собой конъюнкцию ЭД (дизъюнкцию ЭК).
КНФ (ДНФ), каждая ЭК (ЭД) которой содержит каждую переменную списка переменных формулы ровно один раз, называется совершенной КНФ (ДНФ).
Примеры:
 - ЭК;
- ЭК; 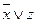 - ЭД;
- ЭД;
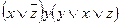 ;
;  ;
;  - КНФ;
- КНФ;
 ;
; 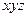 ;
; 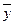 - ДНФ;
- ДНФ;
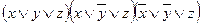 - СКНФ;
- СКНФ;
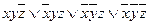 - СДНФ.
- СДНФ.
Алгоритм нахождения совершенных форм с помощью равносильных преобразований:
1. С помощью равносильности (13) [  ] избавимся от всех вхождений эквивалентности в формулу.
] избавимся от всех вхождений эквивалентности в формулу.
2. С помощью равносильности (12) [ 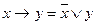 ] избавимся от всех вхождений импликации в формулу.
] избавимся от всех вхождений импликации в формулу.
3. С помощью равносильностей (7. 1) [ 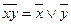 ], (7. 2) [
], (7. 2) [ 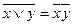 ] и 8 [
] и 8 [  ] избавимся от отрицания над сложными выражениями. В результате мы получим приведенную форму.
] избавимся от отрицания над сложными выражениями. В результате мы получим приведенную форму.
4. С помощью равносильности (4. 2) [ 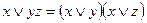 ] ((4. 1) [
] ((4. 1) [ 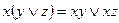 ]), применяя ее до тех пор, пока это возможно, мы получим КНФ (ДНФ).
]), применяя ее до тех пор, пока это возможно, мы получим КНФ (ДНФ).
5. Внедряя в каждую ЭД (ЭК) недостающие переменные по схеме:
ЭД 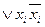 = (ЭД Ú
= (ЭД Ú 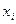 )(ЭД Ú
)(ЭД Ú  ) (ЭК
) (ЭК 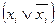 =ЭК
=ЭК 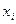 Ú ЭК
Ú ЭК  ) мы получим СКНФ (СДНФ).
) мы получим СКНФ (СДНФ).
Замечания:
· Необходимо учесть, что для тавтологии (формулы тождественно равной 1) не существует СКНФ, а для противоречия (формулы тождественно равной 0) не существует СДНФ.
|
|
|
· Для выполнения некоторых шагов алгоритма, предполагается использование ассоциативности, коммутативности, идемпотентности операций конъюнкции и дизъюнкции, а также законов поглощения.
· Для облегчения алгоритма целесообразно на каждом шаге проверять возможность применения законов идемпотентности и поглощения.
· Иногда бывает целесообразно сначала упростить формулу с помощью основных равносильностей (например, с помощью законов Порецкого), а только затем приступать к выполнению алгоритма. Упрощение формулы может также производится и в нутрии алгоритма.
· Также будем использовать обобщенные законы дистрибутивности:
4. 1. 1. 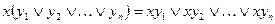
|
4. 2. 1 
|
которые несложно доказываются методом математической индукции.
Алгоритм нахождения совершенных форм с помощью разложения Шеннона:
1. Найдем одномерную таблицу для формулы.
2. Напротив строк, на которых формула принимает значение 1 (0), запишем ЭК (ЭД) так, что если переменная 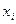 принимает в данной строке значение 1, то она входит в ЭК (ЭД) без отрицания (с отрицанием), в противном случае с отрицанием (без отрицания).
принимает в данной строке значение 1, то она входит в ЭК (ЭД) без отрицания (с отрицанием), в противном случае с отрицанием (без отрицания).
3. Выпишем все полученные ЭК (ЭД) соединяя их знаками дизъюнкции (конъюнкции). В итого мы получим СДНФ (СКНФ).
|
|
|