 |
Тема 11. Частичные булевы функций
|
|
|
|
Тема 11. Частичные булевы функций
Краткая теория
Булева функция называется частичной, если она определена не на всем множестве 
, а лишь на некотором его подмножестве. Частичные функции можно задавать аналогично общим функциям одномерными и двумерными таблицами с учетом того, что соответствующие наборы не пишутся, либо на соответствующих наборах значение функции игнорируется. Особый интерес вызывает задача доопределения частичных булевых функций с целью возможности записи их аналитическими выражениями, а в частности минимизации. Основная идея состоит в том, чтобы так доопределить частичную булеву функцию, чтобы ее МДНФ была самой короткой из всех возможных доопределения.
Примеры решения задач
Задача. Минимизировать частичную булеву функцию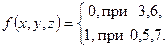 
Решение:
Графический метод.
| x | y | z |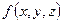 
| |
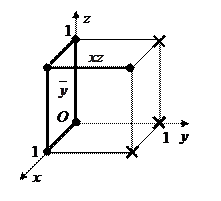Анализируя полученный результата очевидно, что функцию 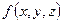необходимо доопределить следующим образом:
| x | y | z |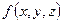
| |
МДНФ: 
.
Аналогично можно проводить рассуждения и для метода Квайна и для метода карт Карно. В общем случае необходим полный перебор всех возможных дополнений.
Упражнения
1. Минимизировать различными методами частичную булеву функцию:
a) 
b)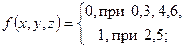 
c)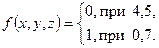 
Дополнительные упражнения
2. Минимизировать методом карт Карно частичную булеву функцию:
|
|
|
a) 
b) 
Тема 12. Различные способы задания графов. Операции над графами
Краткая теория
Граф 
( 
) определяется двумя множествами: V – множество вершин, Е – множество ребер (дуг). Элементы из Е представляют собой неупорядоченные (упорядоченные) пары из V.
Граф содержащий только ребра называется неориентированным графом (неограф), а граф содержащий только дуги – ориентированным графом (орграф).
Операция над графами (без кратных ребер и петель):
1. Дополнением графа (обозначается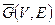 
) называется граф 
множество вершин которого совпадает с множеством вершин исходного графа, а множество ребер (дуг) состоит из всех тех ребер (дуг) которые дополняют данный граф до полного графа.
2. Объединением графов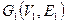 
и 
(обозначается 
) называется граф такой, что 
, 
.
3. Пересечением графов и 
(обозначается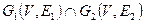 
) называется граф такой, что 
.
4. Соединением (сложением) графов 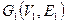и (обозначается 
), при услови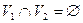и 
и 
называется граф такой, что , 
.
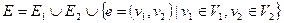5. Удаление вершины 
из графа (обозначается 
) дает граф 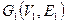такой, что 
, 
.
6. Удаление ребра 
из графа (обозначается 
) дает граф , где 
.
Примеры решения задач
Задача. Для графически заданного графа найти матрицы смежности и инцидентности.
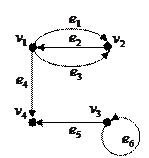| Неориентированный граф |  Ориентированный граф
|
|
Решение:
Матрица смежности графа
| Неориентированный граф | Ориентированный граф |
 
|  
|
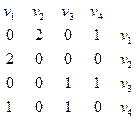
Матрица инцидентности графа
| Неориентированный граф | Ориентированный граф |
 
|  
|
Упражнения
1. Для графа заданного матрицей смежности найти графическое задание и матрицу инцидентности:
a)  ;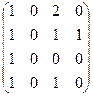
| b)  ;
| c) 
|
2. Для графа заданного матрицей смежности найти графическое задание и матрицу инцидентности:
a)  ;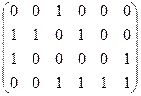
| b)  .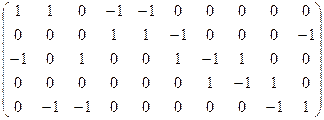
|
3. Выполните действия и найдите соответствующую матрицу смежности для графа :
a) = 
;
|
|
|
b) = 
;
c) = 
;
d) = 
;
e) = 
;
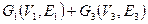f) = ( 
) – 
;
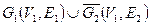g) = ( 
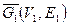) – (1, 3);
где 
, 
, 
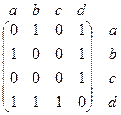
матрицы смежности для графов 
, 
и 
соответственно.
Тема 13. Минимальные деревья
Краткая теория
Деревом называется связный граф без циклов.
Матрицей весов графа называется матрица смежности в ячейках которой стоят веса соответствующих ребер (дуг) и знак бесконечности в случае отсутствия соответствующего ребра.
Минимальным деревом называется остовное дерево графа с минимальным суммарным весом ребер.
Жадный алгоритм построения минимального дерева:
На каждом шаге алгоритма берется ребро с минимальным весом, не образовывающее циклов в строящемся графе.
Алгоритм ближайшего соседа построения минимального дерева:
В качестве исходной берется любая вершина графа. После этого, среди всех ребер инцидентных данной вершине берется ребро с наименьшим весом и включается в строящееся дерево. В дальнейшем к строящемуся дереву добавляются ребра, не образовывающие цикла, инцидентные какой-либо его вершине.
Алгоритм удаления максимальных циклических ребер:
На каждом шаге алгоритма удаляется ребро с максимальным весом образующее цикл в модифицируемом графе.
|
|
|
