Примеры решения задач. Упражнения. Тема 14. Минимальные гамильтоновы циклы. Краткая теория. Алгоритм ближайшего соседа построения минимального дерева:

Примеры решения задач

Задача. Граф  задан матрицей весов:

(2)

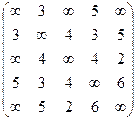. Найти его минимальное дерево тремя способами.

Решение:

Жадный алгоритм построения минимального дерева: (3, 5); (1, 2); (2, 4); (2, 3). При возникновении затруднений исходный граф можно представить графически.

Алгоритм ближайшего соседа построения минимального дерева:

Берем вершину 1.

(1, 2); (2, 4); (2, 3); (3, 5).

 Алгоритм удаления максимальных циклических ребер:

Удаляем ребра: (4, 5); (1, 4); (2, 5); (2, 3).

В итоге получился граф содержащий ребра: (1, 2); (2, 4); (3, 4); (3, 5).

 

Упражнения

1. Построить матрицу весов и минимальное дерево тремя способами для взвешенного графа , если известны координаты его вершин, а вес ребер определяется как квадрат расстояния между точками, определяющими его вершины. . Вершины имеют координаты: (1, 0); (2, 5); (4, 1); (4, 4); (5, 0); (5, 4). (  - полный граф с n вершинами).

2. Найти минимальное дерево тремя способами для графа заданного матрицей весов и определить его вес:

a) ;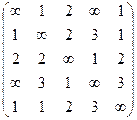

b) ;

c) .

 

Тема 14. Минимальные гамильтоновы циклы

Краткая теория

Гамильтоновым циклом называется элементарный цикл проходящий через все вершины графа.

Граф называется гамильтоновым, если он содержит гамильтонов цикл.

Степенной последовательностью графа называется список степеней его вершин.

Достаточные условия гамильтоновости графа:

1. Теорема (Хватал). Граф со степенной последовательностью  является гамильтоновых, если для всякого k, удовлетворяющего неравенствам , из того, что следует .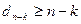

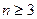2. Теорема (Оре). Если для любой пары несмежных вершин  и  графа G порядка  выполняется неравенство 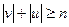, то G – гамильтонов граф.

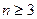3. Теорема (Дирак). Если для любой вершины  графа G порядка  выполняется неравенство 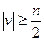, то G – гамильтонов граф.

Самое сильное условие 1. Два других являются его следствиями. Самое слабое условие 3, но оно самое простое для проверки.

 

Примеры решения задач

Задача. Проверить, является ли граф гамильтоновым и в случае положительного ответа найти его минимальный гамильтонов цикл. Граф задан матрицей весов:

.

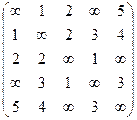Решение:

Выпишем степенную последовательность вершин: 3, 3, 3, 3, 3.

Т. к. , то выполнены все условия теоремы Дирака и граф является гамильтоновым (в противном случае пришлось бы проверять другие теоремы).

 

 

 

Таким образом, минимальным гамильтоновым циклом будет: (1, 2), (2, 5), (5, 4), (4, 3), (3, 1) и его вес равен 11.

 

Упражнения

1. Построить матрицу весов, проверить достаточное условие существования и построить минимальный гамильтонов цикл для взвешенного графа , если известны координаты его вершин, а вес ребер определяется как квадрат расстояния между точками, определяющими его вершины. 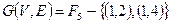. Вершины имеют координаты: (0, 1); (2, 6); (3, 0); (4, 4); (5, 0); (5, 3).

2. Проверить, является ли граф гамильтоновым и в случае положительного ответа найти его минимальный гамильтонов цикл. Граф задан матрицей весов:

.

 

Дополнительные упражнения

3. Построить матрицу весов, проверить достаточное условие существования и построить минимальный гамильтонов цикл для взвешенного графа , если известны координаты его вершин, а вес ребер определяется как квадрат расстояния между точками, определяющими его вершины. 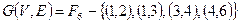. Вершины имеют координаты: (0, 0); (0, 6); (2, 3); (3, 1); (4, 6); (5, 3).

 

Тема 15. Кратчайшие пути на графе

Краткая теория

Длиной пути из вершины  в вершину  графа  называется сумма весов всех его ребер. Для нахождения кратчайшего пути будем использовать алгоритм Дийкстра. Он заключается в следующем:

1. Вершине  присваивается постоянная метка 0, а остальным вершинам временные метки ¥.

2. Всем вершинам, смежным с вершиной  (принадлежащим ), присваиваются метки равные весам ребер соединяющих их с вершиной .

¼

2k+1. Среди всех вершин, имеющих временные метки, выбирается вершина с наименьшей меткой, и данная временная метка становится постоянной.

2k+2. Всем вершинам, смежным с вершиной помеченной последней постоянной меткой, присваиваются новые временные метки равные , где 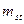– старая метка,  – последняя постоянная метка,  – вес ребра соединяющего данную вершину с вершиной получившей последнюю постоянную метку.

¼

Процесс заканчивается, когда вершина получит постоянную метку, которая и есть искомая величина.

В результате выполнения алгоритма мы попутно получаем минимальные пути от данной вершины до всех вершин имеющих постоянные метки.

Аналогично находится кратчайший путь и ориентированном графе.

 

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: