 |
Примеры решения задач. Упражнения. Тема 15. Эйлеровы графы. Краткая теория. Кратчайший путь, таким образом, имеет вид: a ® d ® b ® e ® g и он равен 18
|
|
|
|
Примеры решения задач
Задача. Найти кратчайший путь из вершины а в вершину g для графа  :
:
 |
Решение:
| a | b | c | d | e | f | g | h |
 (0) (0)
| ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ |
| (0) | ¥ | ¥ | ¥ | ¥ | |||
| (0) |  7 7
|  (3) (3)
| ¥ | ¥ | ¥ | ¥ | |
| (0) | (3) | ¥ | ¥ | ||||
| (0) |  11 11
| (6) | (3) | ¥ | ¥ | ||
| (0) | (6) | (3) | ¥ | ¥ | |||
| (0) |  (9) (9)
| (6) | (3) | ¥ | ¥ | ||
| (0) | (9) | (6) | (3) | ¥ | |||
| (0) | (9) | (6) | (3) | (11) | ¥ | ||
| (0) | (9) | (6) | (3) | (11) | |||
| (0) | (9) | (6) | (3) |  (13) (13)
| (11) | ||
| (0) | (9) | (6) | (3) | (13) | (11) | ||
| (0) | (9) | (6) | (3) | (13) | (11) | (18) |
Кратчайший путь, таким образом, имеет вид: a ® d ® b ® e ® g и он равен 18.
Упражнения
1. Найти кратчайший путь из вершины  в вершину
в вершину  для графа
для графа  :
:

2. Найти матрицу кратчайших пути между вершинами графа  , заданного матрицей весов:
, заданного матрицей весов:
d) 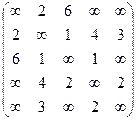 ; ;
| e)  ; ;
| f) 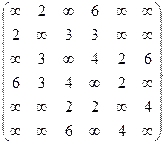
|
Тема 15. Эйлеровы графы
Краткая теория
Цикл, проходящий через все ребра графа, называется эйлеровым. Граф называется эйлеровым, если он содержит эйлеров цикл.
Признак эйлеровости графа: связный граф эйлеров тогда и только тогда, когда степени всех его которого четны.
Алгоритм нахождения Эйлерова цикла состоит из двух этапов.
Первый этап: Пометка ребер.
1. Выберем в графе элементарный цикл и все его ребра пометим числом 1.
¼
k. Выберем в графе элементарный цикл содержащий только непомеченные ребра так, чтобы хотя бы одно его ребро было смежно с помеченным ребром и пометим все его ребра числом k.
¼
Процесс продолжим до тех пор, пока все ребра графа не будут занумерованы
Второй этап: Построение цикла.
|
|
|
В качестве начального выберем ребро с меткой 1. После этого будем присоединять к строящемуся циклу ребра так, чтобы они имели максимальные метки. Процесс завершится, когда все ребра графа будут включены в цикл.
Данный алгоритм используется также для отыскания минимального разбиения графа цепями. Суть решения данной задачи сводится к тому, что если все вершины, имеющие нечетную степень, соединить ребрами с новой вершиной, то в результате мы получим эйлеров граф и для отыскания минимального разбиения достаточно удалить введенную вершину со всеми инцидентными ей ребрами из построенного эйлерового цикла, при этом он распадется на цепи образующие минимальное разбиение.
Количество различных эйлеровых циклов графа равно  , где k – количество элементарных циклов входящих в эйлеров цикл.
, где k – количество элементарных циклов входящих в эйлеров цикл.
Примеры решения задач
Задача. Найти эйлеров цикл для графа  :
:
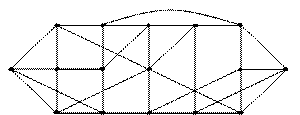
Решение:


Упражнения
1. Найти эйлеров цикл и их количество для графа заданного матрицей смежности:
a)  ; ;
| b)  ; ;
| c)  . .
|
Список используемой литературы
1. Белоусов А. И., Ткачев С. Б. Дискретная математика: Учебник для вузов. – М.: Издательство МГТУ им. Н. Э. Баумана, 2004. – 744 с.
2. Горбатов В. А. Дискретная математика: Учебник для студентов втузов. – М.: Издательство АСТ, 2003. – 447 с.
3. Емельянов А. С. и др. Лекции по теории графов. – М.: Наука, 1990. – 348 с.
4. Иванов Б. Н. Дискретная математика. Алгоритмы и программы: Учебное пособие. – М.: Лаборатория Базовых Знаний, 2003. – 288 с.
5. Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. – М.: Физматлит, 1995. – 256 с.
6. Новиков Ф. А. Дискретная математика для программистов. – СПб.: Питер, 2002. – 304 с.
7. Редькин Н. П. Дискретная математика: Курс лекций для студентов механиков. – СПб.: Лань, 2003. – 96 с.
8. Яблонский С. В. Введение в дискретную математику: Учебное пособие для вузов.. – М.: Высшая школа, 2003. – 384 с.
|
|
|
|
|
|


