 |
Упражнения. Дополнительные упражнения. Тема 9. Полные системы булевых функций. Краткая теория. Примеры решения задач. 8. Выяснить каким классам принадлежит функция:
|
|
|
|
Упражнения
6. Доказать замкнутость классов 
, 
, 
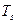и 
.
7. Найти функции двойственные к функциям:
| a) f = 0; | b) f = 1; | c)  ;
|
d)  ;
| e)  ;
| f)  ;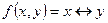
|
g) 
;
h) 
.
8. Выяснить каким классам принадлежит функция:
a)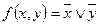 
;
b) 
;
c) 
;
d)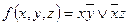 
;
e)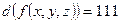 
;
f)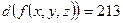 
.
Дополнительные упражнения
9. Найти все самодвойственные функции от двух и от трех аргументов.
10. Выяснить каким классам принадлежит функция:
a) 
;
b) 
.
Тема 9. Полные системы булевых функций
Краткая теория
Система булевых функций является полной, если любая булева функция может быть представлена как формула над данной системой.
| x | y | 
| 
|
Теорема (Поста о полноте). Для того, чтобы система булевых функций была полной необходимо и достаточно, чтобы она содержала хотя бы одну функцию не принадлежащую 
, хотя бы одну функцию не принадлежащую , хотя бы одну функцию не принадлежащую 
, хотя бы одну функцию не принадлежащую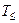 
, хотя бы одну функцию не принадлежащую 
,
– штрих Шеффера.
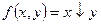– стрелка Пирса (функция Вебба).
Примеры решения задач
Задача. Доказать, что система функций 
является полной и выразите через данные функции функцию .
Решение:
Функция 
принадлежит лишь классам , , а значит не принадлежит классам , , 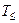(доказать самостоятельно).
Из предыдущей темы нам известно, что функция 
принадлежит классу и не принадлежит классам , , , .
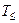Таким образом, по теореме Поста о полноте, данная система функций является полной.
В общем случае проблема выражения конкретной функции через данные, весьма трудоемка. В простейших случаях можно воспользоваться одномерными таблицами.
| x | y | 
|  
| 
|
|
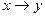
Таким образом
|
|
|
.
Иногда удобно сводить выражение данной функции к функциям, вывод которых уже известен.
Упражнения
1. Выяснить какие из данных систем функций являются полными: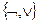 
; 
; 
; 
; 
; ; 
; 
; 
; 
; 
; 
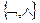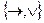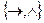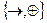
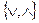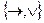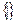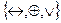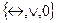и в положительном случае выразить через них функции: 
, 
, 
, 
, 
, 
, 
, 
, 
, 
.
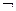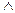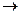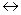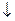2. Какие из данных систем функций являются полными:
a) 
;
b)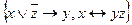 
;
c)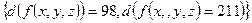 
;
d) 
;
e)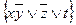 
;
f) 
.
Дополнительные упражнения
3. Приведите пример функции от пяти аргументов, образующую полную систему функций.
Тема 10. Схемы из функциональных элементов и контактно релейные схемы
Краткая теория
Функциональный элемент это устройство, имеющее n входов и один выход. На каждый из входов может подаваться два вида сигналов: 0 или 1, при этом на выходе также генерируется сигнал либо 0, либо 1. Основными функциональными элементами являются: инвертор (реализует отрицание), конъюнктор (реализует конъюнкцию) и дизьюнктор (реализует дизъюнкцию).
| Инвертор | Конъюнктор | Дизьюнктор |
| 
| 
|
Контактно-релейные схемы представляют собой последовательно-параллеьные конструкции контактов (переключателей). Каждый контакт идентифицируется некоторой переменной либо ее отрицанием. Различают два соединений контактов: последовательный (реализует конъюнкцию) и параллельный (реализует дизъюнкцию).
| последовательное соединение | параллельное соединение | |||
| 
|
.
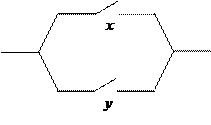
Примеры решения задач
Задача. Найти схему из функциональных элементов и контактно-релейную схему для булевой функции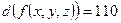 
.
Решение:
Для построения схем найдем сначала МДНФ.
Одна из МДНФ будет иметь вид 
(доказать самостоятельно).
| Схема из функциональных элементов: | Контактно-релейная схема: |
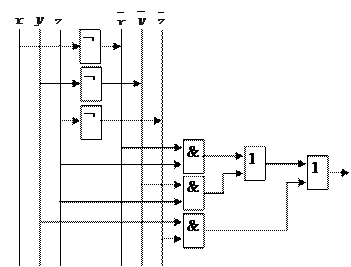
Упражнения
1. Найти схему из функциональных элементов и контактно-релейную схему для булевой функции:
|
|
|
a) 
;
b) 
.
c) 
;
d) 
.
e) 
.
Дополнительные упражнения
2. Найти схему из функциональных элементов и контактно-релейную схему для:
a) полусумматора;
b) полного сумматора;
c) полувычитателя;
d) полного вычитателя.
Полусумматор – это устройство, имеющее два входа и два выхода, реализующее сложение цифр двоичной системы счисления.
Полный сумматор – это устройство, имеющее три входа и два выхода, реализующее сложение цифр двоичной системы счисления с учетом переноса единицы нижнего разряда.
Полувычитатель – это устройство, имеющее два входа и два выхода, реализующее вычитание цифр двоичной системы счисления.
Полный вычитатель – это устройство, имеющее три входа и два выхода, реализующее сложение цифр двоичной системы счисления с учетом заема единицы верхнего разряда.
| Полусумматор | Полный сумматор | Полувычитатель | Полный вычитатель |
| 
| 
| 
|
|
|
|
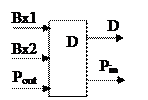
