 |
Свойства чатотных характеристик
|
|
|
|
Свойства чатотных характеристик
1. Непрерывность.
ЧХ, АЧХ, и ФЧХ – непрерывные (или кусочно-непрерывные) функции частоты по определению.
2. Периодичность.
ЧХ, АЧХ, и ФЧХ – периодические функции частоты с периодом, равным частоте дискретизации 
.
3. Четность АЧХ и нечётность ФЧХ.
Если коэффициенты [1Ф – вещественные числа (а другие случаи мы и не рассматриваем), то модуль частотной характеристики (АЧХ)является чётной, а аргумент (ФЧХ) – нечётной функцией частоты:
;
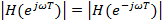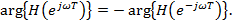
Напомним, что чётной называется функция, которая не изменится при изменении знака аргумента. Если же при изменении знака аргумента изменяется знак функции, но её абсолютное значение сохраняется неизменным, функция называется нечётной.
Доказательство.
Запишем частотную характеристику в виде:
или коротко:
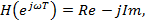
Где вещественная часть – чётная
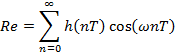
а мнимая – нечётная функция частоты:
Т. к. первом случае имеем сумму косинусов (чётных функций), а во втором – синусов (нечётных функций). Изменив знак аргумента 
получим:
Для модуля частотной характеристики справедливо равенство:
Следовательно АЧХ – чётная функция частоты. Для аргумента частотной характеристики, принимая во внимание, что арктангенс – нечётная функция, справедливы равенства:
;
Следовательно, ФЧХ – нечётная функция частоты.
Связь частотной характеристики с передаточной функцией
Сравним передаточную функцию с частотной характеристикой. Очевидна их взаимосвязь: Частотная характеристика (ЧХ) 
совпадает с передаточной функцией (ПФ) 
, если область значений переменной z на комплексной z-плоскости ограничена точками на единичной окружности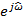 
:
|
|
|
Это позволяет при известной передаточной функции путём подстановки 
автоматически получить частотную характеристику в виде:
Основная полоса частот
Наименование «основная полоса частот» возникло в результате того, что при дискретизации аналогового сигнала его спектр по условию теоремы Котельникова ограничивается верхней частотой
,
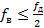Вследствие чего спектры дискретных сигналов, а также частотные характеристики ЛДС имеет смысл рассматривать только в диапазоне 
, который и назвали основным диапазоном или основной полосой частот.
Напомним, что в зависимости от используемой шкалы частот основная полоса соответствует областям:
АЧХ и ФЧХ рассчитывают и изображают на графике в основной полосе частот, при необходимости их легко продолжить на любом интервале частот, учитывая свойства периодичности, а также чётности АЧХ и нечётности ФЧХ.
Единицы измерения частоты, которые используются в системах дискретного времени
Как правило, для описания частотной характеристики систем дискретного времени пользуются двумя единицами измерения частоты – 
(рад/с) и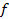 
(Гц). Если частота измеряется в рад/с, частотная характеристика пробегает значения от 
до 
или, что эквивалентно, от до 
(поскольку 
если пользоваться стандартной единицей измерения частоты, которая выражается в герцах, частотный диапазон будет от 0 до 
или от 0 до 1/2Т. Обе эти единицы измерения частоты можно записать в нормированном виде, т. е. при Т=1 или, что эквивалентно, 
. Взаимосвязь между этими двумя единицами измерения частоты показана в таблице. Следовательно, представляющие интерес частотные интервалы можно выразить одним из следующих эквивалентных способов:
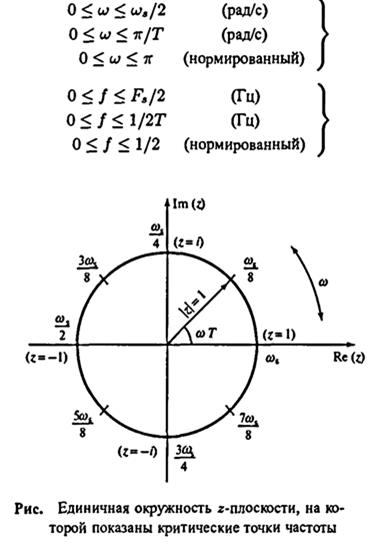
Измерение частоты в герцах больше привлекает (и меньше запутывает), если пользоваться графиками частотной характеристики или спецификацией системы дискретного времени. Однако при оценке численных математических формул в ЦОС удобнее пользоваться величинами, выраженными в рад/с.
|
|
|
|
|
|
