 |
Сохранить выполненное задание в файл с именем «PZ_2_familia studenta.xmcd»
|
|
|
|
Сохранить выполненное задание в файл с именем «PZ_2_familia studenta. xmcd»
Контрольные вопросы:
1. Какой сигнал называется аналоговым, как он может быть описан?
2. Какой сигнал называется дискретным, как он может быть описан?
3. Какой сигнал называется цифровым, как он может быть описан?
4. Что такое частота дискретизации?
5. Сформулировать теорему Котельникова.
6. Что такое частота Найквиста?
7. Что такое отсчеты?
8. Что такое спектр сигнала?
9. Чем отличаются спектры аналогового и дискретного сигналов?
10. Что такое основная полоса частот, нормированные частоты?
11. Что такое квантование?
12. Как произвести восстановление исходного аналогового сигнала по набору его дискретных отсчетов?
Литература
|
|
Практическая работа №3.
Преобразование Фурье (ДПФ и БПФ).
Цель работы
Рассмотреть и вычислить преобразование Фурье на практическом примере.
Задание
1. Осуществить быстрое преобразование Фурье (БПФ) с прореживанием по времени (вычислить 8-точечное ДПФ с помощью двух 4-точечных ДПФ и объединительной операции “бабочка”)
2. Выполнить прямое вычисление 8- точечного ДПФ.
3. Сравнить результаты вычисления (графики) ДПФ п. 1 и п. 2
4. Вычислить преобразование Фурье с помощью встроенных функций MathCAD.
Теоретические сведения
Методические рекомендации
|
|
|
- задаться моделью аналогового сигнала (экспоненциальный импульс) и построить график:
, 
; 
;
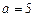- выбрать для данного сигнала 
;
- осуществить дискретизацию сигнала по времени и построить график дискретного сигнала:
;
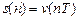Вычисление 8-точечное ДПФ с помощью двух 4-точечных ДПФ и объединительной операции “бабочка”
Произвести прореживание во времени исходной последовательности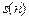 
Для этого:
- осуществить преобразование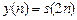 
и построить график 
последовательности с четными номерами 
, 
;
- осуществить преобразование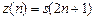 
и построить график 
последовательности с нечетными номерами 
, 
;
- вычислить 4-точечное ДПФ для последовательности с чётными номерами 
:
, 
;
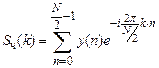- построить график отсчётов амплитудного спектра 
;
- вычислить 4-точечное ДПФ для последовательности с нечётными номерами 
:
, ;
- построить график отсчётов амплитудного спектра 
;
- вычислить вращающийся множитель: 
;
- окончательное вычисление отсчётов спектра дискретного сигнала с использованием операции объединения результатов двух 4 - точечных ДПФ (“бабочки” БПФ) для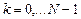 
:
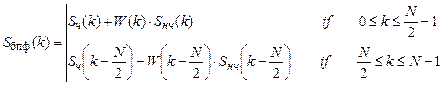
- построение графика 
, ;
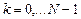Прямое вычисление 8- точечного ДПФ
, ;
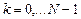Встроенных функций MathCAD для вычисления преобразование Фурье
Огромный пласт задач вычислительной математики связан с расчетом интегралов Фурье для функций, либо заданных таблично (например, представляющих собой результаты какого-либо эксперимента), либо функций, проинтегрировать которые аналитически не удается. Поэтому для решения таких задач применяют численные методы интегрирования, связанные с дискретизацией подынтегральной функции и называемые потому дискретным преобразованием Фурье.
В численном процессоре MathCAD дискретное преобразование Фурье для действительных и комплексных данных реализовано при помощи популярного алгоритма быстрого преобразования Фурье (БПФ). Этот алгоритм реализован во встроенных функциях MathCAD:
|
|
|
fft(y) – вектор прямого преобразования Фурье
ifft(w) – вектор обратного преобразования Фурье
cfft(y) – вектор прямого комплексного преобразования Фурье
icfft(w) - вектор обратного комплексного преобразования Фурье
y – вектор действительных или комплексных данных, взятых через равные промежутки значений аргумента; должен иметь ровно 2n элементов, где n – целое число; если число данных не совпадает со степенью 2, то необходимо дополнить недостающие элементы нулями.
w – вектор действительных или комплексных данных, взятых через равные промежутки значений частоты.
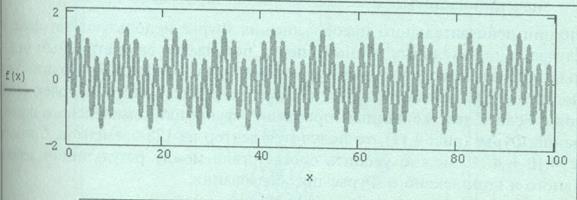
Рисунок 1. – Исходная функция
Рисунок 2. – Спектр функции действительных данных
Рисунок 3. – Спектр функции комплексных данных
Функции действительного преобразования Фурье используют тот факт, что в случае действительных данных спектр получается симметричным относительно нуля и выводят только его половину. Поэтому, в частности, по 128 действительным данным будет получаться всего 65 точек спектра Фурье. Если к тем же данным применить функцию комплексного преобразования Фурье, то получится вектор из 128 элементов. Сравнивая рисунки 2 и 3 можно уяснить соответствие между результатами преобразования Фурье для действительных данных и для комплексных.
Сохранить выполненное задание в файл с именем «PZ_3_familia studenta. xmcd»
Контрольные вопросы:
13. Что такое ряд Фурье?
14. Записать ряд Фурье для аналогового и дискретного сигнала
15. В чем заключается вычислительная сложность ряда Фурье?
16. Что такое поворачивающийся множитель, его свойства?
17. Как ускорить вычисление ДПФ? Суть алгоритма БПФ.
18. Перечислить встроенные функции MathCAD для вычисления преобразования Фурье.
|
|
|
