Типы избирательных фильтров и задание требований к ним

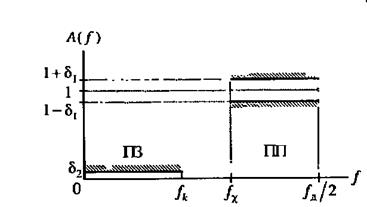
1. Фильтр нижних частот (ФНЧ) имеет три частотных полосы (рис. П. 3. б): полосу пропускания (ПП), полосу задерживания (ПЗ), или ослабления (рис. 17. 3. в) и затухания (рис. 17. 3. г), и переходную полосу. Полоса пропускания(ПП) ограничивается частотой среза f_x; ширина полосы пропускания ∆ f_пп=f_x;

 

δ, — максимально допустимое отклонение от 1 (рис. 17. 3, б);

 

a_max — максимально допустимое ослабление (рис. 17. 3, в) в полосе про-

пускания

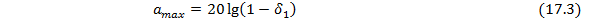
Соответственно максимально допустимое затухание в полосе пропускания (рис. 17. 3, г) имеет вид:

 

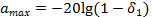
Важным является то обстоятельство, что в соответствии с методом синтеза КИХ—фильтров отклонение АЧХ от 1 (соответственно a(f) от 0) задается симметрично

1-δ ₁≤ A(f)≤ 1+δ ₁‚ а для БИХ-фильтров отклонение задается только в одну сторону так, чтобы АЧХ не превышала единицы. Полоса задерживания (ослабления) (ПЗ) лежит в пределах от граничной частоты f_k до половины частоты дискретизации fд/2:

ее ширина ∆ f_ПЗ = fд / 2-f_k;

δ ₂ —— максимально допустимое отклонение АЧХ от 0;

a₀ — максимально допустимое Ослабление в полосе задерживания

 

 

а в терминах характеристики затухания a₀ — минимально допустимое затухание в полосе задерживания

 

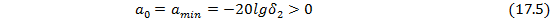
Переходная полоса располагается между полосами пропускания и задерживания, ее ширина ∆ f = f_k - f_x. Поскольку в этой полосе требования не задаются, удовлетворительным окажется любое решение если оно соответствует требованиям в полосах пропускания и задерживания.

 

 

 

2. Фильтр верхних частот (ФВЧ) имеет, как и ФНЧ, Три частотных полосы, которые расположены в обратном, относительно ФНЧ, порядке (рис. 17. 4):

 

полоса задерживания в пределах от 0 до f_k, ∆ f_ПЗ = f_k;

 

переходная полоса в пределах от f_k до f_x. ∆ f = f_x - f_k;

 

палат пропускания в пределах от f_x до fд/2‚ f_ПП = fд/2 - f_x.

 

Остальные параметры определяются так же, как и для ФНЧ.

 

 

 

3. Полосовой фильтр (ПФ) характеризуется пятью частотными полосами (рис. 17. 5), из которых центральная - полоса пропускания, две полосы задерживания и две переходных полосы. Отрицательный индекс частоты означает, что частота расположена слева от середины полосы пропускания. На рис. 17. 5, б обозначены:

 

f _-k - граничная частота первой полосы задерживания ПЗ1, ширина которой ∆ f_ПЗ1 =f _-k;

 

f _–x - левая частота среза полосы пропускания:

 

f_x — правая частота среза полосы пропускания, ширина полосы пропускания ∆ f_ПП = f_x – f _-x;

 

f_k — граничная частота второй полосы задерживания ПЗ2, шприца которой ∆ f_ПЗ2= fд/2 - f_k

 

Переходные полосы 1 и 2 имеют ширину ∆ f₁ = f _–x – f _-k и ∆ f₂ = f_k - f_x соответственно.

 

 

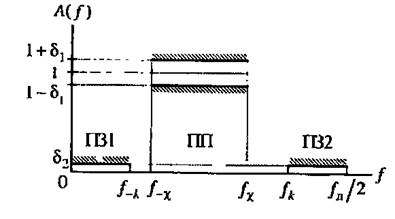
4. Режекторный фильтр (РФ), иногда называемый полосно-заграждающим подобно ПФ характеризуется пятью полосами (рис. 17. 6)‚ из которых две полосы пропускания, одна полоса задерживания и две переходных полосы. Отрицательный индекс частоты означает, что частота расположена слева от середины полосы запоминания. На рис. 17. 6, 6 обозначены:

 

f _–x - частота среза первой полосы пропускания‚ ширина которой ∆ f_ПП1 = f _–x ;

f _-k и f_k - нижняя и верхняя граничные частоты полосы задерживания, ∆ f_ПЗ = f_k - f _–k;

f_x - частота среза второй полосы пропускания, ширина которой ∆ f_ПП2 = fд/2 – f_x.

Переходные полосы 1 и 2 имеют ширину ∆ f₁ = f _–k – f _–x и ∆ f₂ = f_x - f _k, соответственно.

Сохранить выполненное задание в файл электронного бланка под именем

«PZ_9_familia studenta. xmcd»

 

Контрольные вопросы:

1. Что такое цифровой фильтр?

2. Как когут быть реализованы цифровые фильтры?

3. Типы частотно-избирательных фильтров.

4. Что такое оптимальный синтез?

5. Условия безыскаженной передачи сигналов во временной области.

6. Условия безыскаженной передачи сигналов в частотной области.

7. Условия, при которых КИХ-фильтр обладает линейной ФЧХ.

8. Условие симметрии коэффициентов передаточной функции ( и отсчетов импульсной характеристики)

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: