 |
Взаимосвязь между передаточной функцией и разностным уравнением
|
|
|
|
Взаимосвязь между передаточной функцией и разностным уравнением
; 
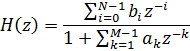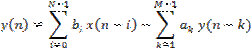
Из сопоставления передаточной функции общего вида и разностного уравнения понятна их взаимосвязь при нулевых начальных условиях:
§ числитель ПФ связан с отсчётами воздействия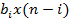 
РУ:
· Задержка отсчёта 
отображается в ПФ степенью 
;
· коэффициент 
сохраняется.
Символически это можно записать следующим образом:
;
§ знаменатель ПФ связан с отсчётами реакции 
и 
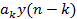РУ:
· свободный член знаменателя всегда равен 1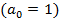 
, в РУ он соответствует реакции :
· задержка отсчёта 
отображается в ПФ степенью;
· у коэффициента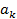 
изменяется знак.
Символически это можно записать следующим образом:
Оценка устойчивости. Критерии устойчивости
по импульсной характеристике
Рассмотрим критерий, позволяющий оценить устойчивость ЛДС по ее импульсной характеристике.
Для того, чтобы линейная дискретная система (ЛДС) была устойчива, необходимо и достаточно, чтобы выполнялось условие абсолютной сходимости ряда
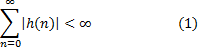
Критерий (1) позволяет утверждать, что не рекурсивные ЛДС (КИХ- системы) принципиально устойчивы, поскольку их импульсная характеристика конечна.
Рекурсивные ЛДС требуют проверки на устойчивость, при этом импульсная характеристика устойчивой рекурсивной ЛДС имеет характер затухающей функции времени.
по передаточной функции
В z-области, где основной характеристикой ЛДС является передаточная функция - z-изображение импульсной характеристики существует критерий, позволяющий оценить устойчивость ЛДС по передаточной функции.
Для того, чтобы линейная дискретная система (ЛДС) была устойчива, необходимо и достаточно, чтобы все полюсы ее передаточной функции находились внутри круга единичного радиуса комплексной z- плоскости или совпадали с нулями передаточной функции, которые находятся на единичной окружности.
|
|
|
Критерий (1) справедлив, если передаточная функция вида
не содержит сокращающихся множителей (когда нуль равен полюсу), в противном случае необходимо обратить внимание на сокращающиеся множители: если полюсы (и равные им нули) расположены внутри единичного круга, ЛДС будет устойчива, иначе – не устойчива.
простая проверка на устойчивость
Система неустойчива, либо минимальной устойчива, если z-образ системы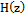 
нельзя разложить на множители (найти достаточное количество значений импульсной характеристики и построить их график, вычислив обратное z- преобразование)
Пример 1. Построение диаграммы нулей и полюсов:
Выразим 
через положительные показатели степени 
, а затем разложим её таким образом, чтобы можно было найти полюсы и нули. Если умножить числитель и знаменатель на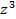 
- самую высокую степень , получится:
В результате разложения получаем:
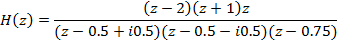
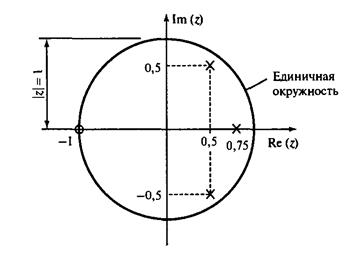
Следовательно, полюсы находятся в точках z = 0. 5 ± 0. 5i и в точке z = 0. 75.
Нули – в точках z = 2, z = -1 и z = 0.
Соответствующая диаграмма нулей и полюсов изображена ниже, на рисунке
Пример 2. Нахождение импульсной характеристики фильтра
1. с помощью метода разложения в степенной ряд;
2. воспользовавшись единичным импульсом системы.
Решение.
1) С помощью метода разложения в степенной ряд значения импульсной характеристики можно найти таким образом:
Исходя из коэффициентов, вычислим значения импульсной характеристики:
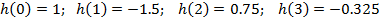
2) Во-первых, исходя из передаточной функции, нужно найти разностное уравнение фильтра:
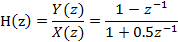
Выполнив перекрёстное умножение и воспользовавшись свойством задержки z - преобразования, найдём разностное уравнение:
|
|
|
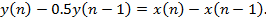
После упрощения получаем:
Теперь импульсную характеристику фильтра можно найти, сделав замену 
где
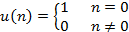
и предположив существование начального условия 
:
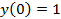
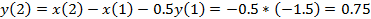
Отсюда значения импульсной характеристики равны:
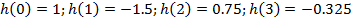
Видно, что оба метода приводят к одинаковым результатам.
|
|
|
