 |
Сохранить выполненное задание в файл с именем «PZ_7_familiastudenta.xmcd»
|
|
|
|
Сохранить выполненное задание в файл с именем «PZ_7_familiastudenta. xmcd»
Контрольные вопросы:
- С помощью каких методов можно оценить частотную характеристику системы дискретного времени?
- Назовите основную характеристику ЛДС в частотной области
- Что такое АЧХ (определение), как ее вычислить?
- Что такое ФЧХ (определение), как ее вычислить?
- Дать несколько определений КЧХ
- Перечислить основные свойства частотных характеристик
- Что такое основная полоса частот? Каким областям она соответствует?
- Какое звено называют фазовым?
- Обоснуйте необходимость применения фазового корректора в каналах связи. Что из себя представляет фазовый корректор?
- Что такое минимально-фазовое и неминемально-фазовое звено?
Литература
|
|
Практическая работа №7.
КИХ-фильтры с линейной ФЧХ.
Типы частотно-избирательных фильтров.
Цель работы
Изучить и построить АЧХ и ФЧХ КИХ- фильтров.
Сделать выводы о возможной реализации частотно-избирательных фильтров.
Задание
1. По заданной передаточной функции найти комплексную частотную характеристику (КЧХ) и построить графики АЧХ и ФЧХ.
2. Для каждого КИХ- фильтра сделать вывод о возможной реализации частотно-избирательного фильтра.
Передаточные функции КИХ-фильтра:
а) ФЧХ 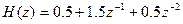
б) ФЧХ 
в) ФЧХ 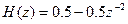
г) ФЧХ ч 
Теоретические сведения
|
|
|
Методические рекомендации
Фильтр - это система или сеть, избирательно меняющая форму сигнала (амплитудно-частотную или фазово-частотную характеристику). Основными целями фильтрации являются улучшение качества сигнала (например, устранение или снижение помех), извлечение из сигналов'информации или разделение нескольких сигналов, объединенных ранее для, например, эффективного использования доступного канала связи.
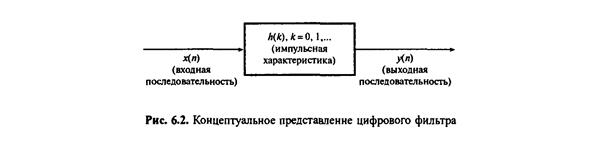
Упрощенная блок-схема цифрового фильтра реального времени с аналоговым входом и выходом приведена на рис. 6. 1. Узкополосный аналоговый сигнал периодически выбирается и конвертируется в набор цифровых выборок, x(n), n = 0, 1, ... . Цифровой процессор производит фильтрацию, отображая входную последовательность x(n) в выходную у(n) согласно вычислительному алгоритму фильтра. ЦАП конвертирует отфильтрованный цифровым образом выход в аналоговые значения, которые затем проходят аналоговую фильтрацию для сглаживания и устранения нежелательных высокочастотных компонентов.

Цифровые фильтры разделены на два обширных класса: фильтры с бесконечной импульсной характеристикой (БИХ-фильтры) и фильтры с конечной импульсной характеристикой (КИХ-фильтры). Фильтр каждого типа (в стандартной форме) можно представить через коэффициенты его импульсной характеристики h(k) (k: 0, 1,... ), как показано на рис. 6. 2. Входной и выходной сигналы фильтра связаны через операцию сверки, данная связь приведена в формуле (6. 1) для БИХ-фильтра и в формуле (6. 2) для КИХ-фильтра.
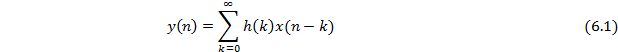

Из данных уравнений понятно, что для БИХ-фильтров импульсная характеристика имеет бесконечную длительность, тогда как для КИХ-фильтра она конечна, поскольку МК) для КИХ—фильтра может принимать всего N значений. На практике вычислить выход БИХ-фильтра с использованием уравнения (6. 1) невозможно, поскольку длительностьимпульсного отклика слишком велика (теоретически — бесконечна). Взамен этого уравнение БИХ фильт- рации переписывается в рекурсивной форме
|
|
|

где a(k) и b(k) — коэффициенты фильтра. Таким образом, уравнения (6. 2) и (6. 3) — это раз-
ностные уравнения КИХ- и БИХ-фильтров соответственно. Данные уравнения (и в част—
ности значения h(k) для КИХ—фильтра или a(k) и b(k) для БИХ-фильтра) используются во
многих задачах разработки фильтров. Отметим, что в уравнении (6. 3) текущая выходная
выборка у(n) является функцией предыдущих выходов‚ а также текущей и предыду-
щих входных выборок, так что БИХ-фильтр — это в некотором роде система с обратной
связью. Сделав этот вывод, стоит внимательнее присмотреться к уравнению для КИХ-фильтра, в котором текущая выходная выборка у(n) зависит только от прошедших и текущего входных значений. Отметим, впрочем, что если положить все b(k) равными нулю, уравнение (6. 3) сводится к уравнению (6. 2). В уравнениях (6. 4, а и 6) приведены альтернативные представления (через передаточные функции) КИХ— и БИХ-фильтров соответственно, причем такие описания очень удобны при оценке частотных характеристик фильтров (подробнее см. главы 4, 7 и 8).
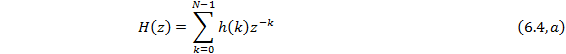

Цифровой фильтр в узком смысле - это частота-избирательная цепь, которая обеспечивает селекцию цифровых сигналов по частоте. К таким фильтрам относятся: фильтры нижних частот (ФНЧ), фильтры верхних частот (ФВЧ), полосовые фильтры (ПФ), режек-торные фильтры (РФ).
На рисунке представлены идеальные АЧХ фильтров: ФНЧ (фильтр низких частот), ФВЧ (фильтр высоких частот), ПФ (полосового) и РФ (режекторного) фильтров
| Идеальная АЧХ фильтра нижних частот (ФНЧ) | 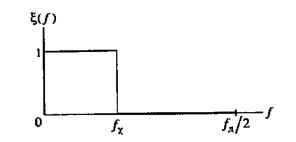
|
| Идеальная АЧХ фильтра верхних частот (ФВЧ) | 
|
| Идеальная АЧХ режекторного фильтра (РФ) | 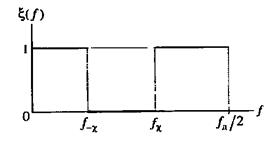
|
| Идеальная АЧХ полосового фильтра (ПФ) | 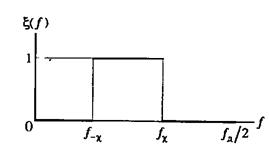
|
Идеальные АЧХ фильтров, вследствие их физической невозможности, необходимо аппроксимировать заранее определенными ограничениями или допусками. (Аппроксимация, или приближение — научный метод, состоящий в замене одних объектов другими, в каком-то смысле близкими к исходным, но более простыми). Все ограничения и допуски составляют требования, предъявляемые к фильтру.
|
|
|
Требования к фильтрам включают в себя:
· задание частоты дискретизации fд [Гц] и типа избирательности (НЧ, ВЧ и т. д. );
· задание требований к АЧХ А(f) или к характеристике ослабления (затухания) а(f)‚ представляющей собой логарифмическую АЧХ. При этом необходимо помнить, что:
o задание требований начинается с установки всех граничных частот фильтра только в основной полосе частот 0≤ f ≤ fд/2;
o Требования в переходных полосах избирательных фильтров не задаются;
o Требования формулируются в вице допустимых отклонений от нормированной АЧХ А(f) [или от а(f)] в полосах пропускания и задерживания и отображаются на диаграмме допусков;
o АЧХ А(f) является безразмерной величиной и выражается в абсолютных единицах;
o характеристики ослабления и затухания обозначаются одинаково, а(f)^2, размерность, а(f) выражается в децибелах, связь между А(f) и характеристикой ослабления а(f) определяется формулой

а при отображении требований в виде характеристики затухания

выбор метода аппроксимации АЧХ A(f) (или a(f)).
|
|
|


