 |
Прежде чем переходить к линейным дискретным системам, мы изучает математический аппарат z-преобразования (прямое, обратное, способы его нахождения)
|
|
|
|
Литература
|
|
Прежде чем переходить к линейным дискретным системам, мы изучает математический аппарат z-преобразования (прямое, обратное, способы его нахождения)
ПЗ- примеры нахождения z-преобразования разными способами для одного и того же звена, а также нахождение решения задачи по исходным данным, заданным графически.
ПЗ- примеры, разобранные в предыдущем ПЗ, необходимо решить с помощью встроенных функций и операторов MathCAD + индивидуально для каждого примерчик для самостоятельного разбора, использование двух способ из трех разобранных
Практическая работа № 4.
Линейные дискретные системы (ЛДС) во временной области.
Цель работы
Исследование линейных дискретных систем во временной области (вычисление реакций при разных воздействиях)
Задание
- Вычислить реакцию ЛДС по формулам свертки при нулевых начальных условиях. Сравнить. Построить графики импульсной характеристики, входного воздействия, реакции, вычисленной по формуле свертки
Импульсная характеристика
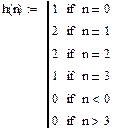
| Входное воздействие на ЛДС
|
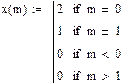
- Вычислить реакцию ЛДС в случае ее описания разностными уравнениями. (Найти импульсную характеристику и реакцию при заданном воздействии)
| Разностное уравнение | Воздействие 1 | Воздействие 2 |
2. 1 
| 
| 
|
2. 2 
|
| 
|
|
|
|
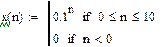
Теоретические сведения
Методические рекомендации
Системой обработки сигналов (системой) называется объект, выполняющий требуемое преобразование входного сигнала в выходной. Входной сигнал системы называется воздействием, выходной - реакцией. Соотношение вход/выходотображает взаимосвязь между входным x(nT) и выходным y(nT) сигналами ЛДС, т. е. реакцию ЛДС на произвольное воздействие.
Во временной области соотношение вход/выход ЛДС описывается линейными уравнениями:
- Формулой свёртки (свёрткой), если используется импульсная характеристика;
- Разностным уравнением, если используются параметры ЛДС.
- Линейное уравнение (1) называется формулой свёртки (свёрткой).
(1)
Выполнив в (1) замену переменных, можно получить другой вариант записи формулы свёртки:
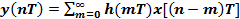(2)
Для нормированного времени формулы (1) и (2) принимают вид соответственно:
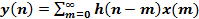(3)
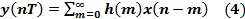
Взаимосязь между воздействием 
и реакцией 
также может описываться линейным разностным уравнением:
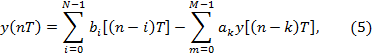
где:
коэффициенты (вещественные константы), внутренние параметры ЛДС;
воздействие и реакция;
значения задержек для воздейстия и реакции соответственно;
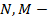константы;
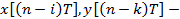воздействие и реакция, задержанные на 
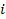и 
периодов дискретизации соответственно.
Для нормированного времени разностное уравнение (5) принимает вид:
Линейная дискретная система называется рекурсивной, если хотя бы один из коэффициентов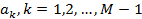 
разностного уравнения (6) не равен нулю.
Линейная дискретная система называется нерекурсивной, если хотя бы один из коэффициентов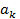 
разностного уравнения (6) равны нулю.
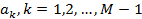
Для не рекурсивной ЛДС разностные уравнения принимают вид:
Пример
Вычислить импульсную характеристику не рекурсивной ЛДС второго порядка, соотношение вход/выход которой описывается РУ
|
|
|
|
|
|
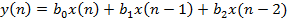
