 |
Пример. Решение. Методические рекомендации. Вычисление частотной характеристики с помощью БПФ. Встроенных функций MathCAD для вычисления преобразование Фурье
|
|
|
|
Пример
Дано описание частной характеристики полосового фильтра дискретного времени в виде
Полоса пропускания 6 – 10 кГц,
Полосы подавления 0 – 4 и 12 – 16 кГц,
Частота дискретизации 32 кГц.
А. Выразите через нормированную частоту f.
Б. Переведите спецификацию из стандартных единиц (Гц) в рад/с.
В. Переведите спецификацию из рад/с (п. Б) в нормированную частоту 
.
Решение
1. Граничные частоты, которые измеряются в Гц, можно записать в нормированном виде, просто разделив каждую из них на частоту дискретизации. Таким образом, спецификация в нормированном виде будет выглядеть так:
Полоса пропускания 0, 1875 – 0, 3125,
Полосы подавления 0 – 0, 125 и 0, 375 – 0, 5,
Частота дискретизации 1.
2. Поскольку 
, для того, чтобы перейти к рад/с, каждая граничная частота просто умножается на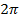 
. Теперь спецификация частотной характеристики будет следующей:
Полоса пропускания 
Полосы подавления 
Частота дискретизации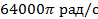 
.
3. Граничные частоты из п. 2 можно записать в нормированном вид, разделив каждую из них на 32 кГц (частоту дискретизации), например,
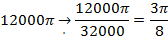
Таким образом, спецификация приводится к виду:
Полоса пропускания 
Полосы подавления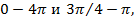 
Частота дискретизации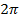
Методические рекомендации
Нахождение частотных характеристик методом подстановки в пакете MathCAD:
- в передаточную функцию звена сделать подстановку z=ejw
- записать полученную частотную характеристику H(w)
- найти амплитудно-частотную характеристику (АЧХ) по формуле A(w)=|H(w)|
- найти фазочастотную характеристику (ФЧХ) по формуле φ (w)=argH(w)
- построить графики АЧХ и ФЧХ.
Вычисление частотной характеристики с помощью БПФ
Для оценки частотной характеристики систем дискретного времени также можно использовать БПФ. Для БИХ – систем это делается следующим образом: сперва находится импульсная характеристика системы, например, методом разложения в степенной ряд, а затем вычисляется БПФ импульсной характеристики. Такая последовательность действий связана непосредственно с уравнением
|
|
|
которое показывает, что частотная характеристика системы дискретного времени – это просто Фурье-образ её импульсной характеристики. Чтобы частотная характеристика получилась гладкой, прежде, чем искать БПФ, важно взять достаточное количество значений импульсной характеристики и/или дополнить значения импульсной характеристики нулями.
Вычисление частотной характеристики с помощью БПФ в пакете MathCAD:
- для найденных значений импульсной характеристики электронного бланка «PZ_6_blank. xmcd» вычислить БПФ;
- в результате вычисления БПФ получится вектор комплексных значений КЧХ. Например, массив А. Далее следует сформировать два вектора: первый (например, А1) должен содержать действительные части комплексных чисел массива А, второй (например, А2) – мнимые части комплексных чисел массива А.
- Исходя из определений АЧХ и ФЧХ
,
записать равенства и построить графики АЧХ и ФЧХ.
Встроенных функций MathCAD для вычисления преобразование Фурье
Огромный пласт задач вычислительной математики связан с расчетом интегралов Фурье для функций, либо заданных таблично (например, представляющих собой результаты какого-либо эксперимента), либо функций, проинтегрировать которые аналитически не удается. Поэтому для решения таких задач применяют численные методы интегрирования, связанные с дискретизацией подынтегральной функции и называемые потому дискретным преобразованием Фурье.
В численном процессоре MathCAD дискретное преобразование Фурье для действительных и комплексных данных реализовано при помощи популярного алгоритма быстрого преобразования Фурье (БПФ). Этот алгоритм реализован во встроенных функциях MathCAD:
|
|
|
fft(y) – вектор прямого преобразования Фурье
ifft(w) – вектор обратного преобразования Фурье
cfft(y) – вектор прямого комплексного преобразования Фурье
icfft(w) - вектор обратного комплексного преобразования Фурье
y – вектор действительных или комплексных данных, взятых через равные промежутки значений аргумента; должен иметь ровно 2n элементов, где n – целое число; если число данных не совпадает со степенью 2, то необходимо дополнить недостающие элементы нулями.
w – вектор действительных или комплексных данных, взятых через равные промежутки значений частоты.
Рисунок 1. – Исходная функция
Рисунок 2. – Спектр функции действительных данных
Рисунок 3. – Спектр функции комплексных данных
Функции действительного преобразования Фурье используют тот факт, что в случае действительных данных спектр получается симметричным относительно нуля и выводят только его половину. Поэтому, в частности, по 128 действительным данным будет получаться всего 65 точек спектра Фурье. Если к тем же данным применить функцию комплексного преобразования Фурье, то получится вектор из 128 элементов. Сравнивая рисунки 2 и 3 можно уяснить соответствие между результатами преобразования Фурье для действительных данных и для комплексных.
|
|
|
