 |
Сохранить выполненное задание в файл с именем «PZ_4_familia studenta.xmcd»
|
|
|
|
Решение
Согласно определению, ИХ – это реакция на цифровой единичный импульс поэтому, выполнив замену
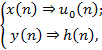
Перепишем РУ в виде:
и решив его методом прямой подстановки при нулевых начальных условиях:
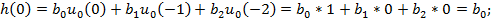
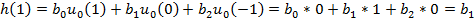
при n> 3
Распространяя полученные результаты на не рекурсивную ЛДС произвольного порядка, приходим к следующим выводам:
1. Импульсная характеристика не рекурсивной ЛДС имеет конечную длительность
2. Значения отсчётов ИХ равны коэффициентам разностного уравнения
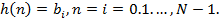
Поэтому рекурсивные ЛДС называют системами с конечной импульсной характеристикой (КИХ-системами).
Пример 1
Вычислить импульсную характериску рекурсивной ЛДС первого порядка, соотношение вход/выход которой описывается РУ
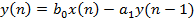
Решение. Выполним замену, перепишем РУ в виде:
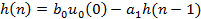
и решим его методом прямой подстановки при нулевых начальных условиях:
…
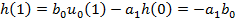
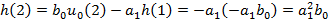
Вычисление их можно продолжать бесконечно по формуле:
Распространяя полученные результаты на не рекурсивную ЛДС произвольного порядка приходим к следующим выводам:
1. Импульсная характеристика не рекурсивной ЛДС имеет конечную длительность;
2. Значения отчётов ИХ равны коэффициентам разносного уравнения
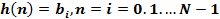
Пример 2
Решить разностное уравнение 
методом прямой подстановки при заданном воздействии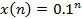 
и нулевых начальных условиях. Вычислить пять отсчётов реакции.
| Воздействие | Реакция |
| 
| |
| 
| |
| 
| |
| 
| |
| 
|
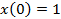
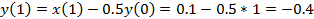
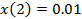
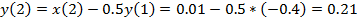
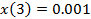
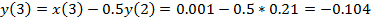
Сохранить выполненное задание в файл с именем «PZ_4_familia studenta. xmcd»
Контрольные вопросы:
- Назовите основную характеристику ЛДС во временной области.
- Для чего нужны формулы свертки?
- Что такое разностное уравнение?
- Назовите признаки БИХ_ и КИХ-систем
- Какая ЛДС называется рекурсивной (не рекурсивной)?
Литература
|
|
|
|
|
Практическая работа № 5.
Описание линейных дискретных систем в z-области.
Цель работы
Исследование линейных дискретных систем в z-области.
Задание
- Построить карту нулей и полюсов передаточной функции для каждого звена
- Построить импульсную характеристику для каждого звена
- Произвести анализ звеньев на устойчивость
Теоретические сведения
Методические рекомендации
При выборе варианта задания необходимо руководствоваться номером в журнале и последним номером в зачетной книжке. Итого, для анализа ЛДС в z-области у каждого студента должно быть два звена.
При анализе рассматриваемых звеньев на устойчивость использовать следующие клише: «Звено устойчиво, потому что…. 1)…. 2)….. 3)», «Звено не устойчиво, потому что…1).. 2)…3).. »
Уметь определять и обосновывать порядок рассматриваемых звеньев, их тип (минимально-фазовое, не минимально-фазовое звено)
| Номер варианта | Тип звена |
| |
| |
| |
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
|
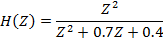
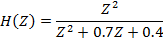
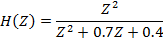
В Z-области основной характеристикой ЛДС является z-изображение импульсной характеристики h(n), которое определяется с помощью Z-преобразования и называется передаточной функцией.
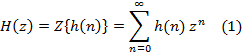
По известному z-изображению импульсная характеристика h(n) находится с помощью обратного Z-преобразования.
Передаточной функцией H(z) линейной дискретной системы называется отношение z-изображения реакции к z-изображению воздействия при нулевых начальных условиях.
|
|
|
Передаточная функция, не зависящая ни от реакции, ни от воздействия, а выраженная через внутренние параметры ЛДС (коэффициенты разностного уравнения)
Как любая дробно-рациональная функция, ПФ (3) характеризуется своими особыми точками (полюсами) и нулями.
Нулями называются значения z, при которых ПФ(3) равна нулю.
Особыми точками (полюсами) называют значения z, при которых знаменатель ПФ равен нулю.
Нули и полюсы передаточной функции удобно изображать в виде точек на комплексной z–плоскости. Положение точек определяется их координатами, чаще всего полярными. Нули изображаются кружками ( ° ), а полюсы – звёздочками (*). Совокупность нулей ( ° ) и полюсов (*) на z–плоскости называется картой нулей и полюсов.
|
|
|
