 |
Методы расчета коэффициентов КИХ-фильтра
|
|
|
|
Методы расчета коэффициентов КИХ-фильтра
Напомним, что КИХ-фильтр характеризуется следующими уравнениями:

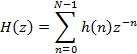
Единственной целью большинства методов вычисления (или приближенного вычисления) коэффициентов КИХ-фильтров является получение значений h(n), при которых фильтр удовлетворяет спецификациям, в частности, относящимся к амплитудно-частотной характеристике, и требованиям к пропускной способности. Разработано несколько методов получения h(n). Наиболее широко используемыми из них являются метод вырезания, оптимальный метод и метод частотной выборки. Все три метода позволяют получать КИХ-фильтры с линейной фазовой характеристикой.
Метод взвешивания (метод вырезания, метод окон)
В данном методе используется факт, что частотная характеристика фильтра HD(w)
и соответствующая импульсная характеристика hD(n) связаны обратным преобразованием Фурье:
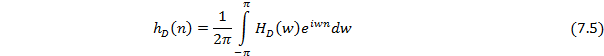
Индекс D используется, чтобы различать идеальную и практическую импульсные характеристики. Необходимость такого разделения станет понята несколько позже. Если HD(w) известна, hD(n) мощно получить, применив преобразование Фурье к обеим частям уравнения (7. 5). Для иллюстрации предположим, что требуется разработать фильтр нижних частот.
Допустив, что характеристика идет от –wc до wc, упрощаем интегрирование и получаем следующую импульсную характеристику:
 (7. 6)
(7. 6)
(Используем правило Лопиталя)
Импульсные характеристики идеальных фильтров верхних частот, полосовых фильтров и режекторных фильтров также находятся из уравнения (7. 6) и все они приведены в табл. 7. 2. Импульсная характеристика фильтра нижних частот изображена на рис. 7. 4, б, из которого видно, что hD(n) симметрична относительно n=0 (т. е hD(n) = hD(-n)), так что фильтр будет иметь линейную фазовую характеристику. Описанный простой подход связан с некоторыми проблемами. Характеристика hD(n) уменьшается при удалении от точки n=0, она длится теоретически до n = ±∞. Следовательно, полученный фильтр не является КИХ-фильтром.
|
|
|
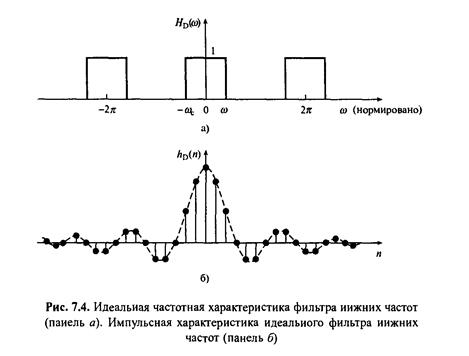
Таблица 7. 2. Идеальные импульсные характеристики стандартных частотно-избирательных фильтров
| ТИП ФИЛЬТРА | hD(n), n≠ 0 | hD(0) |
| Фильтр нижних частот | 
| 2fc |
| Фильтр верхних частот | 
| 1-2fc |
| Полосовой фильтр | 
| 2(f2-f1) |
| Заграждающий фильтр | 
| 1-2(f2-f1) |
Очевидным является решение усечь идеальную импульсную характеристику, положив hD(n) = 0 для n, больше, чем (скажем) М. При этом вводится нежелательная неравномерность и выбросы - имеет место так называемый эффект Гиббса. То, как отбрасывание коэффициентов сказывается на характеристике фильтра, показано на рис. 7. 5. Чем больше коэффициентов осталось, тем ближе спектр фильтра к идеальной характеристике (см. рис. 7. 5, 6 и в). Прямое усечение hD(n)‚ как оно описано выше.
В частотной области это эквивалентно свертке HD(w) с W(w), где W(w) – Фурье-образ W(w). Тогда как W(w) имеет классический вид функции (sin x)/x ‚ усечение hD(n) приводит к появлению в частотной характеристике выбросов.
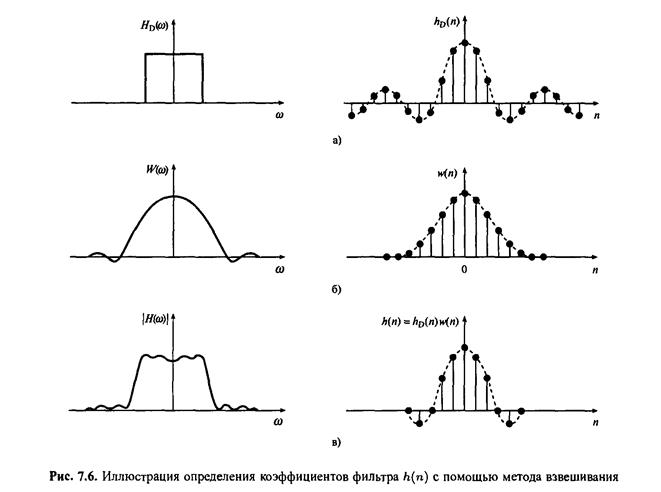
На практике идеальная частотная характеристика пд множится на подходящую весовую функцию w(n) с конечной длительностью. Таким образом, получаюшаяся им-пульсная характеристика гладко затухает до нуля. Данный процесс иллюстрируется на рис. 7. 6. На рис. 7. 6, а показана идеальная частотная характеристика и соответствующая идеальная импульсная харакгеристика. На рис. 7. 6, б показана весовая функция конечной длительности и ее спектр. На рис. 7. 6, в показана функция h(n), которая получается перемножением hD(n) и w(n). Из соответствующей частотной характеристики видно, что неравномерности и выбросы, характерные для прямого усечения, в значительной степени подавлены. В то же время, ширина полосы перехода больше, чем для прямоугольной функции. Известно, что ширина полосы перехода фильтра определяется шириной основного лепестка весовой функции. Боковые лепестки приводят к появлению неравномерности в полосах пропускания и подавления.
|
|
|
|
|
|


