Силы, действующие на жидкость. Давление в жидкости

Основные физические свойства жидкостей

Модели жидкостей

В механике жидкости не рассматривается молекулярное строение жидкости и предполагается, что жидкость заполняет рассматриваемый объем полностью без пустот.

Таким образом, вместо жидкости вводится ее модель, обладающая свойством непрерывности, так называемый континуум.

Введение данной гипотезы позволяет существенно упростить теоретические исследования и рассматривать термодинамические и кинематические параметры жидкости как функции координат точки в пространстве и во времени, причем в большинстве эти функции предполагаются непрерывными и дифференцируемыми.

Математическое описание движения жидкой среды с учетом вязкости, текучести и сжимаемости весьма затруднено и особенно затруднено решение этих уравнений. Вследствие этого, в гидромеханике используют упрощенные модели среды и отдельных явлений.

Наибольшее распространение получили две модели: несжимаемая идеальная(невязкая) жидкость и несжимаемая вязкая жидкость. Пренебрежение свойствами вязкости и сжимаемости позволяет существенно упростить математическое описание и получить многие решения в аналитическом виде. При использовании модели вязкой несжимаемой жидкости получение аналитических решений возможно только для простейших случаев.

С точки зрения механических свойств все жидкости делятся на два больших класса: малосжимаемые (капельные) и сжимаемые (газообразные).

Системы, состоящие из нескольких фаз, называются многофазными. В том случае, если фазы всего две, то системы называются двухфазными. Двухфазные системы получили широкое распространение в технике, и в качестве примера можно назвать следующие (пневмотранспорт); (распылители,);(испарители, эрлифты).В данных примерах основной фазой является непрерывная фаза, а вторая фаза – дискретная фаза. На границах раздела фаз основные теплофизические свойства меняются скачком.

Количество дискретной фазы в двухфазном рабочем теле определяется объемной концентрацией

(1.1.)

гдеV₁ и V₂ –объемы непрерывной и дискретной фаз;

V_{см –} объем двухфазной смеси.

Средняя плотность двухфазного рабочего тела, зная истинные плотности фаз, определится как

 

(1.2)

При расчете течения многофазных сред, производят «размывание» дискретной фазы по объему рабочего тела и после этого применяют аппарат дифференциального исчисления к двум сплошным средам (несущей и несомой).

 

Основные физические свойства жидкости.

 

К основным свойствам жидкости относятся: плотность, вязкость, поверхностное натяжение.

Плотность жидкостей.

 

Под плотностью жидкости понимают массу жидкости, заключенную в единице объема

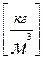, (1.3)

где m – масса жидкости в объеме V.

Если жидкость неоднородна, то формула(1.3) определяет лишь среднее значение плотности в данном объеме.

Плотность среды в произвольной точке определится как

. (1.4)

Предел берется при стягивании объема 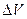к точке.

Наряду с плотностью широко используется понятие удельного объема, который является величиной, обратной плотности

 

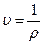. (1.5)

Плотность жидкости меняется с изменением давления и температуры. Эта зависимость существенно различна для капельных жидкостей и газов.

Сжимаемость капельных жидкостей под действием давления характеризуется коэффициентом объемного сжатия 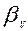[м²/Н] который представляет собой относительное изменение объема жидкости на единицу изменения давления

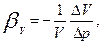[Па^-1] (1.6)

где V – первоначальный объем жидкости.

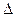V – изменение этого объема при увеличении давления на . При увеличении давления происходит уменьшение объема, чем и объясняется знак минус.

Величина, обратная коэффициенту объемного сжатия, представляет модуль упругости жидкости

E_о = [Па]. (1.7)

Коэффициент 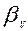и, следовательно, E_о слабо изменяются при изменении температуры и давления для капельных жидкостей и средние значения для воды составляют соответственно

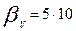^-10 Па^-1; E_о= 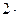10⁹Па.

Прочность жидкости на разрыв весьма мала и в практических расчетах не учитывается.

Температурное расширение капельных жидкостей характеризуется коэффициентом температурного расширения, выражающим относительное увеличение объема жидкости при увеличении температуры на .

. (1.8)

Коэффициент температурного расширения для капельных жидкостей незначителен и для воды при температуре от 283 ^оК до 293 ^оК и давлении 0,1 МПа составляет

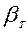=0,00015 1/^оК.

С учетом выше изложенного, изменение плотности жидкости при изменении температуры запишется в виде

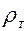= _о , (1.9)

Т_о, _о – температура и плотность при нормальных условиях. Нормальные условия: t=0 ^оС, 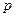=1ат.=10⁵ Па.

В отличие от капельных жидкостей газы характеризуются значительной сжимаемостью и высокими значениями коэффициента температурного расширения. Зависимость плотности газа от давления и температуры устанавливается уравнением состояния.

Для идеального газа (газ, в котором не учитывается взаимодействие между молекулами) справедливо уравнение состояния Клапейрона-Менделеева

, (1.10)

где 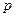- абсолютное давление [Па]; R – газовая постоянная [для воздуха R=287 Дж/кг_*гдад]; Т – абсолютная температура[^оК].

При других условиях плотность газа определяется по формуле

(1.10а)

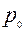, _о,T_о – параметры газа при стандартных условиях; Т₀ – 293^оК, Р=10⁵ Па.

Для изотермического процесса

(Т=const) из формулы (1,10) имеем

, (1.10б)

а для адиабатического процесса

=const, (1.10в)

где 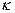= 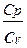- показатель адиабаты.

Важной характеристикой, определяющей зависимость изменения плотности газа при изменении давления в движущейся среде, является скорость распространения звука а

. . (1.10г)

Для воздуха

При Т= 293^оК, а=342 м/с, в воде а=1480 м/с.

Газ можно считать несжимаемым при скоростях движения, не превышающих 100 м/с.

 

Вязкость жидкости.

 

Свойство жидкостей оказывать сопротивление сдвигу называется вязкостью. При движении жидкости происходит относительное перемещение частиц, что приводит к появлению силы трения между ними, причем количественное значение ее пропорционально вязкости жидкости. Рассмотрим движение жидкости вдоль плоской стенки (Рис.1.1).

 

При ламинарном движении жидкости она движется параллельными слоями, скорость которых, вследствие тормозящего эффекта, уменьшается от максимального значения до нуля по мере приближения к стенке.

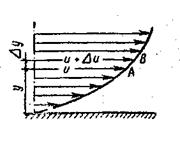Рассматривая два слоя жидкости А и В, расположенных друг от друга на расстоянии , нетрудно видеть, что значение их скоростей отличается на величину 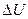. Величина за единицу времени представляет собой абсолютный сдвиг слоя В по слою А, а отношение 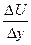представляет градиент скорости или относительный сдвиг.

Рис. 1.1.

 

Силу трения на единицу площади, представляющую величину касательного напряжения, можно определить как

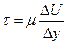. (1.11)

В том случае, если слои будут находиться на бесконечно малом расстоянии друг от друга, величина 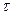определится как

. (1.12)

Коэффициент характеризует сопротивляемость жидкости сдвигу и называется абсолютной или динамической вязкостью.

Впервые на существование зависимости между касательным напряжением и градиентом скорости указал Ньютон и поэтому она называется законом трения Ньютона.

Полную силу трения можно определить как

F= (1.13)

где S – площадь трущихся слоев.

В том случае, если градиент скорости отрицателен, в записанных выше формулах в правой части ставят знак «минус».

Наряду с коэффициентом динамической вязкости в гидрогазодинамике широко используют понятие коэффициента кинематической вязкости

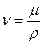[м²/с]. (1.14)

Название кинематическая она получила вследствие того, что в ее размерности отсутствуют единицы силы. Динамическая вязкость имеет размерность [ ], а кинематическая - [м²/с].

Необходимо отметить, что с увеличение температуры вязкость капельных жидкостей уменьшается, причем весьма значительно, а вязкость газов увеличивается. Это объясняется тем, что с увеличением температуры газа интенсивность теплового движения молекул возрастает, что приводит к увеличению вязкости.

В капельных жидкостях молекулы не могут двигаться по разным направлениям, а могут колебаться вокруг своего среднего положения. С увеличением температуры средние скорости колебательных движений молекул увеличиваются, что приводит к ослаблению удерживающих связей и приобретению большей подвижности, а это приводит к уменьшению вязкости.

Для чистой пресной воды зависимость динамической вязкости от температуры определяется по формуле Пуазейля

. (1.15)

С увеличением температуры от 0 до 100 ^оС динамическая вязкость воды уменьшается почти в 7 раз. Вода принадлежит к наименее вязким жидкостям. Наименьшую вязкость имеет жидкая углекислота (в 50 раз меньше вязкости воды).

Для определения вязкости воздуха можно пользоваться формулой

=(1700+5,8t-0.0117t²) . (1.16)

Все эти зависимости получены для так называемых ньютоновских однородных жидкостей, для которых напряжения, вызываемые вязкостью, находятся в линейной зависимости от скорости деформации.

Течение в некоторых жидкостях не подчиняется закону вязкости Ньютона (1. 12). К этим так называемым неньютоновским (или аномальным), жидкостям можно отнести, например, строительный раствор, глинистый раствор, употребляемый при бурении скважин, нефтепродукты при температуре, близкой к температуре застывания и др.

Чтобы привести такие жидкости в движение, необходимо приложить иногда значительное усилие. Движение неньютоновских жидкостей начинается только после того, как касательные напряжения в них достигнут некоторого предельного значения (так называемое начальное напряжение сдвига): при меньших касательных напряжениях эти жидкости не текут, а испытывают только упругие деформации, как твердые тела.

Таким образом, в аномальных жидкостях сила трения возникает еще в покоящихся, но уже стремящихся прийти в движение жидкостях. На рис. 1.2. показана зависимость между касательным напряжением и градиентом скорости.

Вязкость аномальных жидкостей (так называемая структурная вязкость) при заданных температуре и давлении непостоянна и изменяется в зависимости от градиента скорости по мере разрушения структуры жидкости, а следовательно, не является физической константой, как вязкость нормальных жидкостей.

 

 

 

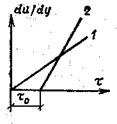Рис. 1.2. Зависимость касательного напряжения от градиента скорости для нормальных 1 и аномальных 2 жидкостей.

 

Движение неньютоновских жидкостей по трубопроводу из условия равновесия внешних и внутренних сил выражается следующей формулой:

 

, ( 1.17)

где 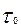- максимальное напряжение сдвига;

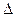р – перепад давления на рассматриваемом участке трубы;

R – внутренний радиус трубы;

– длинна участка трубопровода.

На рис.1.3. приведена зависимость максимального напряжения сдвига от градиента скорости на стенке трубы (, где Q – объемный расход жидкости). Эта зависимость характеризует свойства различных жидкостей.

 

Рис. 1.3. Зависимость максимального напряжения сдвига от градиента скорости на стенке трубы.

 

Линия 1 характеризует вязкость ньютоновских жидкостей. При создании малейшего перепада давления на некотором участке трубы такие жидкости начинают перемещаться.

Линия 2 характеризует вязкость неньютоновской жидкости:

(1.18)

Если жидкость – парафинистая нефть, то с увеличением скорости сдвига связи между частицами парафина все более нарушаются и вязкость уменьшается. Кривые этого вида наблюдаются вблизи температуры застывания нефти. Такие жидкости называются псевдопластическими.

При низких температурах в парафинистой нефти образуется достаточно прочная структурная решетка парафина. Нефть в этом случае приобретает свойство сопротивляться сдвигающим усилиям. Чтобы сдвинуть нефть в трубопроводе, необходимо приложить некоторый начальный перепад давления, т.е. для начала движения жидкости в трубе необходимо, чтобы напряжение сдвига (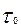) было больше предельного напряжения (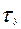) сдвига ( 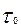> 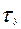). Нефти и жидкости, которые удовлетворяют этим условиям, называются пластическими. При малых перепадах давления такие жидкости не текут. При высокой температуре они могут стать ньютоновскими. Кривая 3 рис. 1.3 характеризует пластическую жидкость.

Напряжение сдвига вязкопластических жидкостей определяется по уравнению Шведова – Бингама:

, (1.19)

где 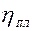- коэффициент пластической вязкости.

Профиль течения вязкопластической жидкости в круглой трубе отличается от профиля течения ньютоновской жидкости. В центре потока жидкость движется в виде твердого цилиндрического ядра.

Радиус ядра r₀ можно определить по формуле:

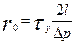. (1.20)

Расход вязкопластичной жидкости по трубопроводу определяется по формуле Букингема:

. (1.21)

Из формулы (1.21) при r₀=0 определяется расход для ньютоновской жидкости.

 

Поверхностное натяжение

При контакте капельной жидкости с другой капельной жидкостью, газом или твердым телом молекулы жидкости, находящейся на поверхности находятся в условиях, которые отличаются от условий, в которых находятся молекулы внутри жидкости, т.к.последних окружают молекулы со всех сторон. Вследствие этого, энергия поверхностных молекул отличается от энергии молекул в объеме жидкости на величину, называемую поверхностной энергией. Эта энергия пропорциональна площади поверхности раздела S

Э_п= S, (1.22)

где – коэффициент поверхностного натяжения, зависящий от природы соприкасающихся сред.

Коэффициент поверхностного натяжения можно представить в виде

= (1.23)

где F – сила поверхностного натяжения; l -длина линии, ограничивающей поверхность раздела.

Поверхностное натяжение жидкости чувствительно к ее чистоте и температуре. При увеличении температуры поверхностное натяжение жидкости уменьшается, а в критической точке, где отсутствует различие между паром и жидкостью равно нулю.

Смачивающаяся способность жидкости на границе раздела трех фаз: жидкой, твердой и газообразной, определяется величиной краевого угла. Величина краевого угла зависит от природы соприкасающихся сред и не зависит от формы поверхности и силы тяжести. В том случае, если краевой угол >90^о, жидкость считается несмачивающей. Если <90^о, жидкость считается смачиващей (Рис.1.4).

 

 

Смачивающая Несмачивающая

 

Рис. 1.4.

 

Гидростатика

Силы, действующие на жидкость. Давление в жидкости

 

Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практические приложения.

Из механики твердого тела известно, что в том случае, если на тело не действуют внешние силы или их сумма равна нулю, то тело находится в состоянии покоя или прямолинейного равномерного движения. Данное утверждение справедливо и для жидкости. В этом случае отсутствует взаимное перемещение частиц жидкости и такое состояние массы жидкости называется равновесным.

Все внешние силы, действующие на жидкость, можно разделить на массовые (объемные) и поверхностные.

Массовые силы – это силы, величина которых пропорциональна массе (силы тяжести, силы инерции).

Поверхностные силы – это силы, действующие на поверхность S ограничивающую объем V, со стороны окружающей жидкости. К ним относятся: силы давления и силы трения. Эти силы непрерывно распределены по поверхности жидкости и пропорциональны площади этой поверхности.

В общем случае поверхностная сила R, действующая на площадке S, направлена под некоторым углом к ней, и ее можно разложить на нормальную F и тангенциальную T составляющие (Рис.2.1).

 

Рис.2.1. Разложение поверхностной силы на две составляющие.

 

Первая называется силой давления, а вторая – силой трения.

Массовые силы отнесенные к единице массы, а поверхностные к единице площади называют единичными силами.

Так как массовая сила равна произведению массы на ускорение, следовательно, единичная массовая сила равна соответствующему ускорению.

Единичная поверхностная сила, называемая напряжением поверхностной силы, раскладывается на нормальные и касательные напряжения.

Нормальное напряжение называется давлением гидромеханическим, а в случае покоя – гидростатическим и обозначается буквой р.

Если сила давления F равномерно распределена по площадке S, то среднее давление определяется по формуле

р= 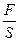. (2.1)

Давление в данной точке равно

р= . (2.2)

Если давление р отсчитывается от абсолютного нуля, то его называют абсолютным, а если отсчитывается от атмосферного давления р_а, то его называют избыточным или манометрическим(р_м).

Следовательно

р_абс=р_а+р_м.

Таким образом, манометрическое давление – это превышение давления в данной точке над атмосферным

р_м=р_абс-р_а.

 

12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: