 |
Истечение жидкости через насадки
|
|
|
|
В том случае, если стенка, через отверстие в которой происходит истечение, имеет значительную толщину по сравнению с размерами отверстия, то характер истечения существенным образом меняется, поскольку стенка влияет на направление струи. Аналогичный эффект наблюдается, если к отверстию в тонкой стенке присоединить короткую трубку того же диаметра, что и отверстие. Такие трубки длиной не менее 2,5-3 диаметров отверстия называются насадками или соплами. Присоединение насадка к отверстию изменяет расход вытекающей жидкости, и следовательно, изменяет время опорожнения сосуда.
Рассмотрим наружный цилиндрический насадок (рис. 7.5). Струя жидкости при входе в насадок сжимается, затем расширяется и заполняет все его сечение. В промежутке между сжатым сечением и стенками насадка образуется вихревая зона. Так как струя выходит из насадка полным сечением, то коэффициент сжатия струи 
=1, а коэффициент расхода 
, т.е. для насадка коэффициент расхода и коэффициент скорости имеют одинаковую величину.
Рис. 7.5
Составим уравнение Бернулли для сечения 1-1 и 2-2, показанных на рис.7.5.
Принимая 
и что
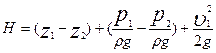, (7.24)
преобразуем уравнение к следующему виду
. (7.25)
Потери напора в насадке складываются из потерь на вход в насадок и на внезапное расширение сжатой струи внутри насадка, т.е.
. (7.26)
Из уравнения неразрывности имеем
. (7.27)
Подставляя выражение (7.27) а формулу (7.26), получим
(7.28)
где 
- коэффициент сопротивления сопла.
Уравнение (7.25) с учетом (7.28) запишется в виде
а скорость истечения из насадка
(2.29)
где введено обозначение
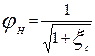. (7.30)
Для расхода получим формулу
.
Сравнивая ее со стандартной формулой 
, приходим к заключению, что
. (7.31)
|
|
|
Таким образом формулы скорости и расхода для насадка имеют тот же вид, что и для отверстия в тонкой стенке, но значения коэффициентов будут другими.
При истечении с большими числами Re (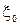
=0), получаем следующее значение коэффициента расхода
0,845. (7.32)
При истечении воды и воздуха в обычных условиях опыт показывает, что
0,82. (7.33)
Сравнивая коэффициенты расхода и скорости для насадка и отверстия в тонкой стенке, видим, что насадок увеличивает расход (более чем на 35%) и уменьшает скорость истечения примерно на 15%.
Действительно, для больших значений Re отношение 
и 
.
Для насадка характерно, что давление в сжатом сечении внутри насадка меньше атмосферного. Для определения величины вакуума в сжатом сечении насадка запишем уравнение Бернулли, связывающее это сечение с выходным сечением
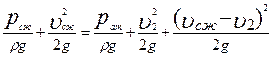, (7.34)
где 
- потери напора на внезапное расширение струи.
Далее получаем
Принимая во внимание, что
имеем 
или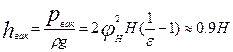 
. (7.35)
При истечении воды обычно принимают 
0,75Н. В соответствии с уравнением (7.35) вакуум зависит от напора, возрастая с его увеличением. Предельное значение величины составляет 10,33м вод. столба, это соответствует предельной величине напора Нпр=11,6м. При увеличении напора сверх Нпр происходит отрыв струи от стенок и насадок начинает работать как отверстие в тонкой стенке (вакуум исчезает).
Гидравлический удар
Явление резкого повышения давления в трубопроводе при внезапном его перекрытии носит название «Гидравлического удара». Процесс этот очень быстротечен, и характеризуется чередованием резких повышений и понижений давления.
Исследование гидроудара в трубах впервые было выполнено Н.Е.Жуковским.
Гидравлический удар, по Н.Е.Жуковскому, представляет собой сложный физический процесс возникновения и распространения ударной волны. Пренебрегая рядом факторов, в том числе потерями напора, процесс гидроудара можно представить так. Пусть из резервуара вытекает поток жидкости и движется по горизонтальной трубе со скоростью 
. На расстоянии 
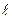от входного сечения (рис.8.1) находится задвижка, которую можно закрыть как угодно быстро.
|
|
|
Предположим, что это закрытие происходит мгновенно. В этом случае частицы жидкости, которые непосредственно соприкасаются с поверхностью задвижки, мгновенно остановятся, затем остановится ближайший к ним слой жидкости. Произойдет очень быстрое сжатие этого слоя, и давление в нем увеличится.
Рис. 8.1
Затем остановится и сожмется следующий слой жидкости, и в нем также увеличится давление, далее сжатие жидкости, сопровождающееся увеличением давления, будет распространяться по всей длине трубы в направлении от задвижки к резервуару.
Пусть за время 
повышенное, т.е. ударное давление достигнет резервуара. Если обозначить расстояние от резервуара до задвижки через 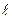, то скорость распространения ударного давления
.
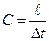Величину С называют скоростью ударной волны. В момент достижения ударной волны входного отверстия вся вода в трубе окажется сжатой, скорости всех частиц равными нулю и давление повышенным против первоначального, т.е. большим давления, которое обусловлено уровнем воды в резервуаре. Вследствие этого начнется отток жидкости из трубы в резервуар и постепенно вся жидкость в трубе придет в движение в направлении к резервуару, что приведет к падению давления до его первоначального значения. Когда это давление достигает задвижки, жидкость движется в трубе в сторону резервуара с некоторой скоростью. В следующий момент времени начинается ее постепенная остановка, начиная от сечения у задвижки, при этом происходит понижение давления. Когда скорость по всей трубе станет равной нулю, пониженное давление достигнет входного сечения трубы. После этого, начинается послойное восстановление движения с первоначальной скоростью в сторону задвижки. Через промежуток времени эту начальную скорость приобретает последний слой жидкости (у задвижки), и явление «гидравлического удара» повторяется. В действительности вследствие того, что стенки трубы обладают упругостью, упругостью также обладает движущаяся жидкость и существует трение между слоями жидкости, колебания в трубопроводе затихают.
|
|
|
Определим величину повышения давления 
в горизонтальной трубе у задвижки при мгновенном ее закрытии. Составим уравнение количества движение для всей массы жидкости в трубопроводе. Количество движения в момент времени t равно
. (8.1)
В момент времени t+ количество движения будет равно нулю, т.к. в этот момент времени все частицы указанной массы останавливаются
.
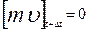Приращение количества движения за время
. (8.2)
Определим сумму импульсов всех сил, действующих на эту массу в течение времени . Импульсы силы тяжести и силы давления со стороны стенок трубы равны нулю, т.к. эти силы нормальны оси трубопровода. Силы давления на торцевые сечения дают в сумме импульс, равный
. (8.3)
Пренебрегая импульсами касательных напряжений вследствие их малости, имеем
,
откуда 
. (8.4)
Принимая во внимание, что 
- скорость распространения ударной волны, величина скачка давления определится по формуле Н.Е.Жуковского
. (8.5)
Таким образом, величина скачка давления 
зависит от начальной скорости движения воды в труде и скорости распространения ударной волны. При абсолютно жестких стенках трубопровода скорость распространения ударной волны совпадает со скоростью распространения звука в жидкости
, где 
- модуль упругости жидкости.
Для воды E0=1,96*109Па и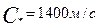 
Для упругих стенок трубопроводов, имеем
, где 
- кажущийся модуль упругости жидкости;
d- диаметр трубы;
Е – модуль упругости материала стенок трубопровода (для стали Е=1,96*1011Па);
- толщина стенок трубопровода.
Таким образом, величина скачка давления определится как
. (8.6)
Анализируя формулу (8.6), можно сделать вывод, что чем < модуль упругости материала стенок и чем > диаметр трубопровода и < толщина стенок, тем < величина гидравлического удара.
Общее время пробега прямой и отраженной волн составляет длительность фазы гидроудара
. (8.7)
Далее циклы повышения и понижения давления будут чередоваться с промежутками времени 
до тех пор, пока под влиянием гидравлических сопротивлений этот колебательный процесс не затухнет.
|
|
|
В том числе, если длительность фазы гидроудара < чем время полного закрытия задвижки 
, то интенсивность скачка давления определится как
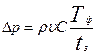. (8.8)
Различают прямой гидравлический удар, если 
и непрямой, если 
.
Способы предотвращения и смягчения гидроудара:
1) устранение возможности прямого гидроудара, что сводится к увеличению времени срабатывания кранов и др. устройств;
2) установкой перед этими устройствами демпфирующих воздушных колпаков, гидроаккумуляторов или предохранительных клапанов.
Для газопроводов и воздухопроводов величина гидроудара обычно мала.
Библиографический список
1. АльтшульА.Д., Животовский Л.С., Иванов Л.П. Гидравлика и аэродинамика. – М.: Стройиздат, 1987-414с.
2. Башта Т.М., Руднев С.С. и др. Гидравлика, гидромашины и гидропроводы: Учебник для вузов. М.: Машиностроение, 1982-423с.
3. Щерба В.Е. Механика жидкости и газа: Учебное пособие – Омск, 1999. – 111с.
4. Киселев П.Г. Гидравлика. Основы механики жидкости: Учебное пособие для вузов. – М.: Энергия, 1980 – 360с.
5. Примеры расчетов по гидравлике: Учебное пособие для вузов (Альтшуль А.Д. и др. – М.: Стройиздат, 1976 – 254с.)
6. Бутаев Д.А., Колмыкова З.А. и др. Сборник задач по машиностроительной гидравлике: Учебное пособие для вузов. Под редакцией Куколевского И.И. – М.: Машиностроение, 1981. – 468с.
7. Идельчик Н.Е. Справочник по гидравлическим сопротивлениям. – М.: Машиностроение, 1975. – 559с.
|
|
|
