 |
Уравнение Бернулли для элементарной струйки идеальной жидкости
|
|
|
|
Рассмотрим установившееся течение идеальной жидкости, находящейся под действием лишь одной массовой силы – силы тяжести, и выведем для этого случая основное уравнение, связывающее между собой давление в жидкости и скорость ее движения.
Возьмем одну из элементарных струек, составляющих поток, и выделим сечениями 1 и 2 участок этой струйки произвольной длины (рис.4.1)
Пусть площадь первого сечения равна dS1, скорость в нем 
1, давление p1, а высота расположения центра тяжести сечения отсчитанная от произвольной горизонтальной плоскости сравнения, z1. Во втором сечении соответственно dS2, 
2, p2 и z2. За бесконечно малый отрезок времени dt выделенный участок струйки переместится в положение 
.
Рис.4.1
Применим к массе жидкости в объеме участка струйки теорему механики об изменении кинетической энергии суть, которой в том, что работа сил, приложенных к телу, равна приращению кинетической энергии этого тела. Такими силами в данном случае являются силы давления, действующие нормально к поверхности рассматриваемого участка струйки, и сила тяжести.
Найдем работу сил давления, силы тяжести и изменение кинетической энергии участка струйки за время dt.
Работа силы давления в первом сечении положительна, т.к. направление силы совпадает с направлением перемещения, и выражается как произведение силы Р1dS1 на путь 
1dt:
P1dS1 1dt.
Работа силы давления во втором сечении имеет знак минус и определяется выражением
- -p2dS2 2dt.
Силы давления, действующие на боковую поверхность струйки, работы не производят, т.к. они нормальны к этой поверхности, а, следовательно, нормальны к перемещениям.
Тогда работа сил давления будет
P1 1dS1dt-p2 2dS2dt. (4.1)
Работа силы тяжести равна изменению потенциальной энергии положения участка струйки, поэтому надо из энергии положения жидкости в объеме 1 – 2 вычесть энергию положения жидкости в объеме . При этом энергия положения промежуточного объема 
сократится, и останется лишь разность энергии элементов 
, 
. Если учесть уравнение расхода (3.3.), то нетрудно заметить, что объемы, а следовательно, и силы тяжести заштрихованных элементов и равны между собой:
|
|
|
. (4.2)
Тогда работа силы тяжести выразится как произведение разности высот на силу тяжести dG:
. (4.3)
Чтобы подсчитать приращение кинетической энергии рассматриваемого участка струйки за время dt, необходимо из кинетической энергии объема вычесть кинетическую энергию объема 1 – 2. При вычитании кинетическая энергия промежуточного объема сократится, и останется лишь разность кинетических энергий элементов и , сила тяжести каждого из которых равна dG.
Таким образом, приращение кинетической энергии равно
. (4.4)
Сложив работу сил давления (4.1) с работой силы тяжести (4.3) и приравняв эту сумму приращению кинетической энергии (4.4), получим
. (4.4’)
Разделив обе части уравнения на dG, и произведя сокращения, получим
или
(4.5)
где z – геометрическая высота, или геометрический напор;
- пьезометрическая высота, или пьезометрический напор;
- скоростная высота, или скоростной напор.
Уравнение (4.5) называется уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости. Трехчлен вида
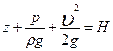называется полным напором.
Уравнение (4.5) записано для двух произвольно взятых сечений и выражает равенство полных напоров Н в этих сечениях. Следовательно, и для любого другого сечения этой же струйки полный напор будет иметь то же значение
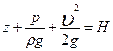=const (вдоль струйки)
Итак, для идеальной движущейся жидкости сумма трех напоров (высот); геометрического, пьезометрического и скоростного есть величина постоянная вдоль струйки.
|
|
|
Это положение иллюстрируется графиком (рис.4.2), где показано изменение всех трех высот вдоль струйки. Линия изменения пьезометрических высот называется пьезометрической линией.
Для горизонтального участка струйки из уравнения Бернулли и уравнения расхода следует, что если площадь поперечного сечения струйки уменьшается, т.е. струйка сужается, то скорость течения жидкости увеличивается, а давление уменьшается, и наоборот.
Рис.4.2. Изменение пьезометрического и скоростного напоров вдоль струйки идеальной жидкости.
Штриховой линией показана пьезометрическая кривая при увеличении расхода в 
раз, вследствие чего скоростные высоты увеличиваются в 2 раза, а в узкой части струйки давление становится меньше атмосферного.
Это была геометрическая интерпретация уравнения Бернулли.
А теперь рассмотрим энергетический смысл уравнения Бернулли.
Разделим уравнение (4.4’) на массу dm участка, равную
и преобразуем уравнение подобно предыдущему. Тогда вместо выражения (4.5) будем иметь
. (4.6)
Условимся называть удельной энергией жидкости энергию, отнесенную к единице массы.
Члены уравнения (4.6) являются различными формами удельной механической энергии жидкости, а именно:
gz – удельная энергия положения, т.к. частица жидкости массой 
, находясь на высоте z, обладает энергией положения равной gz, а на единицу массы приходится энергия 
.
- удельная энергия давления движущейся жидкости;
- удельная потенциальная энергия жидкости;
- удельная кинетическая энергия жидкости;
- полная удельная механическая энергия движущейся жидкости.
Таким образом, энергетический смысл уравнения Бернулли для элементарной струйки идеальной жидкости заключается в постоянстве вдоль струйки полной удельной энергии жидкости. Следовательно, уравнение Бернулли выражает закон сохранения механической энергии в идеальной жидкости.
|
|
|
