 |
Основные дифференциальные уравнения движения идеальной жидкости в форме Эйлера и их интегрирование
|
|
|
|
 Выведем дифференциальные уравнения для произвольной идеальной сжимаемой жидкости, движущейся относительно прямоугольной системы координат OXYZ. Из всей совокупности движущихся частиц выделим в данный момент какую – нибудь частицу жидкости в форме элементарного прямоугольного параллелепипеда (рис. 4.3) со сторонами dx, dy, dz.
Выведем дифференциальные уравнения для произвольной идеальной сжимаемой жидкости, движущейся относительно прямоугольной системы координат OXYZ. Из всей совокупности движущихся частиц выделим в данный момент какую – нибудь частицу жидкости в форме элементарного прямоугольного параллелепипеда (рис. 4.3) со сторонами dx, dy, dz.
Рис. 4.3
Задачу получения динамических уравнений для движущейся жидкости будем решать, используя принцип Даламбера.
Считая, что в данный момент времени бесконечно малая жидкая частица как бы отвердела, остановим ее и рассмотрим условия равновесия этой остановленной частицы. Как известно условиями равновесия являются шесть уравнений равновесия – три уравнения для проекций сил на оси координат и три уравнения для проекций моментов. Чтобы составить эти уравнения, нужно рассмотреть, какие силы действуют на рассматриваемую частицу жидкости.
На грани будут действовать поверхностные силы р1;р2…р6, являющиеся результатом воздействия на частицу окружающей жидкости. Величина каждой из них определится, очевидно, произведением среднего гидродинамического давления р, действующего по соответствующей площадке, на ее площадь dS.
Помимо поверхностных сил, на частицу будут действовать массовые силы, распределенные по всему ее объему, т.е. воздействующие на каждую точку внутри частицы (силы тяжести).
Проекции массовых сил, отнесенных к единице массы частицы, обозначим через X, Y, Z. Тогда, чтобы получить проекции массовых сил, действующих на всю частицу, нужно величины X, Y, Z умножить на массу частицы, равную  . Таким образом, проекции массовой силы могут быть написаны в виде
. Таким образом, проекции массовой силы могут быть написаны в виде

Установив силы, действующие на частицу, для получения уравнений равновесия нужно применить принцип Даламбера. Согласно этому принципу действующие на частицу поверхностные и массовые силы в каждый момент времени уравновешиваются силами инерции. Обозначим через Ux, Uy, Uz проекции скорости бесконечно малой частицы по координатным осям. Тогда проекции ускорения частицы могут быть написаны в виде
|
|
|

Известно, что сила инерции численно равна произведению массы на ускорение, но направлена обратно ускорению. Следовательно, для проекций инерционной силы будем иметь следующие выражения:
 .
.
Для удобства последующих выкладок составим таблицу проекций на координатные оси всех полученных выше сил.
Таблица 4.1
| Силы в проекции на | Поверхностные | Массовые | Инерционные |
| Ось Х Ось Y Ось Z | 


|

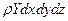

| 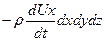

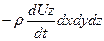
|
Чтобы получить уравнения равновесия, нужно приравнять нулю сумму поверхностных, массовых и инерционных сил. Для этого просуммируем сначала первую строчку таблицы и приравняем сумму нулю, затем то же сделаем с другими. В результате будем иметь следующие три уравнения равновесия:



Далее следовало составить три уравнения для моментов относительно координатных осей. Но мы эти уравнения писать не будем по той причине, что в пределе частица стягивается в точку и все силы будут сходящимися, т.е. уравнения моментов тождественно обратятся в нуль.
Для преобразования полученных трех уравнений вычислим прежде всего разность р1-р2.
Так как давление в идеальной жидкости не зависит от направления, то следовательно, давление по трем взаимно ортогональным бесконечно малым площадкам, проходящим через одну и ту же точку, одинаково. Обозначим его через р.
Тогда, очевидно, р1=р3=р5=р.
Давление р2 на правую грань параллелепипеда, отстоящую от левой грани на расстоянии dx, равно
|
|
|
р2=р+  .
.
Следовательно, искомая разность
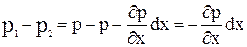 .
. 
Подставив найденное выражение для
 в первое уравнение,
в первое уравнение,
получим
 .
.
Это уравнение можно переписать иначе:

Два другие уравнения получаются аналогично. В результате будем иметь следующую систему дифференциальных уравнений:
 (4.10)
(4.10)
Полученные уравнения являются основными дифференциальными уравнениями движения идеальной жидкости в форме Эйлера. Члены этих уравнений представляют собой соответствующие ускорения, а смысл каждого из уравнений заключается в следующем: полное ускорение частицы вдоль координатной оси складывается из ускорения от массовых сил и ускорения от сил давления.
Учитывая, что

уравнения (4.10) можно записать в виде
 (4.11)
(4.11)
В систему трех уравнений входят пять неизвестных Ux, Uy, Uz, р и  . Поэтому ее необходимо дополнить уравнениями неразрывности и состояния. Эти уравнения применимы как к несжимаемой жидкости, так и к сжимаемой, т.е. к газу. Различие будет только в характере изменения плотности
. Поэтому ее необходимо дополнить уравнениями неразрывности и состояния. Эти уравнения применимы как к несжимаемой жидкости, так и к сжимаемой, т.е. к газу. Различие будет только в характере изменения плотности  . Если жидкость несжимаемая, то
. Если жидкость несжимаемая, то  - величина постоянная; для газа
- величина постоянная; для газа  будет величиной переменной.
будет величиной переменной.
Интегрирование уравнений Эйлера для установившегосядвижения.
Рассматривая установившееся движение жидкости, умножим каждое из уравнения (4.10) на соответствующие проекции элементарного перемещения, равные dx=Uxdt; dy=Uydt; dz=Uzdt, и сложим уравнения.
Получим
 . (4.12)
. (4.12)
Учитывая, что выражение в скобках (4.12) является полным дифференциалом давления, а также, что

Уравнение (4.12) можно переписать в следующем виде
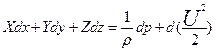 (4.13)
(4.13)
или
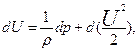 где U- силовая функция.
где U- силовая функция.
Интегрирование этого уравнения выполним для частного случая установившегося движения идеальной жидкости, когда на жидкость действует лишь одна массовая сила – сила тяжести
X=0; Y=0; Z=-g.
Подставляя эти значения в уравнение (4.13), получим
 или
или 
Так как для несжимаемой жидкости  , предыдущее уравнение можно переписать в виде
, предыдущее уравнение можно переписать в виде
 .
.
Это уравнение означает, что приращение суммы трехчленов, заключенных в скобки, при перемещении частицы жидкости вдоль линии тока (траектории) равно нулю. Следовательно, указанный трехчлен есть величина постоянная вдоль линии тока, а, следовательно, и вдоль элементарной струйки, т.е.
 .
.
Таким образом, получили уравнение Бернулли для струйки идеальной жидкости, найденное ранее другим способом.
|
|
|
Если записать это уравнение для двух сечений струйки 1 – 1 и 2 – 2, то оно примет вид выражения (4.5)
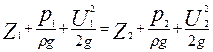 .
.
4.3. Уравнение Бернулли для потока жидкости с поперечнымсечением конечных размеров.
 При переходе от элементарной струйки идеальной жидкости к потоку реальной (вязкой) жидкости, имеющему конечные размеры, необходимо учесть неравномерность распределения скоростей по сечению, а также потери энергии (напора). То и другое является следствием вязкости жидкости. Из–за неравномерного распределения скоростей по поперечному сечению приходится вводить в рассмотрение среднюю по сечению скорость
При переходе от элементарной струйки идеальной жидкости к потоку реальной (вязкой) жидкости, имеющему конечные размеры, необходимо учесть неравномерность распределения скоростей по сечению, а также потери энергии (напора). То и другое является следствием вязкости жидкости. Из–за неравномерного распределения скоростей по поперечному сечению приходится вводить в рассмотрение среднюю по сечению скорость 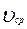 .
.
Для плавно изменяющегося течения уравнение Бернулли, составленное для элементарной струйки, можно распространить на поток с поперечным сечением конечных размеров (в таком потоке скорости в различных точках поперечного сечения различны). Течение называют плавноизменяющимся, если угол расхождения между соседними элементарными струйками настолько мал, что составляющими скорости в поперечном сечении можно пренебречь.
Считаем, что распределение давления по поперечному сечению следует закону гидростатики, т.е. величина  одинакова для всех точек сечения.
одинакова для всех точек сечения.
Поток может быть рассмотрен как совокупность элементарных струек. Энергия каждой отдельной струйки равна
 [
[  ], (4.14)
], (4.14)

ds- площадь элементарной струйки
Энергия для всего потока будет
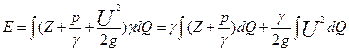 . (4.15)
. (4.15)
Первое слагаемое выражает потенциальную энергию потока
 (4.16)
(4.16)
Второе слагаемое выражает кинетическую энергию. Учитывая, что dQ=Uds, имеем
 (4.17)
(4.17)
Местную скорость U можно представить в виде
 где
где  - средняя скорость жидкости;
- средняя скорость жидкости;
 - разность
- разность  (
( >, <, =0).
>, <, =0).
Выполняя подстановку, получаем
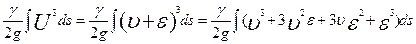 (4.18)
(4.18)
или
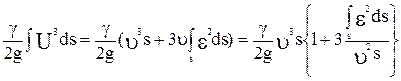 . (4.19)
. (4.19)
Здесь учтено, что  (на половине площади
(на половине площади  >0, а на другой половине
>0, а на другой половине  <0), и что интеграл
<0), и что интеграл  т.к. малая величина
т.к. малая величина  для разных точек сечения имеет различный знак.
для разных точек сечения имеет различный знак.
Вводя обозначение
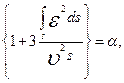 (4.20)
(4.20)
получим следующее выражение для кинетической энергии потока
 (4.21)
(4.21)
В результате для энергии всего потока имеем
|
|
|
Епотока  (4.22)
(4.22)
откуда удельная энергия потока будет
Епотока  . (4.23)
. (4.23)
Таким образом, уравнение Бернулли для потока конечного размера отличается от такового для элементарной струйки тем, что здесь скоростной напор, определяемый средней скоростью, дополнен коэффициентом  ,, носящим название коэффициента Кориолиса.
,, носящим название коэффициента Кориолиса.
 представляет собой отношение действительной кинетической энергии потока в данном сечении к кинетической энергии того же потока и в том же сечении, но при равномерном распределении скоростей.
представляет собой отношение действительной кинетической энергии потока в данном сечении к кинетической энергии того же потока и в том же сечении, но при равномерном распределении скоростей.
Величина этого коэффициента зависит от степени неравномерности распределения скорости по сечению. Этот коэффициент всегда > единицы (за исключением случая, когда местные скорости в данном сечении равны между собой, тогда  =1) и при обычном распределении скоростей равняется
=1) и при обычном распределении скоростей равняется  1,1; во многих практических случаях можно принимать
1,1; во многих практических случаях можно принимать  =1.
=1.
Для потока вязкой жидкости уравнение Бернулли запишется в виде
 . (4.24)
. (4.24)
4.4. Уравнение движения вязкой жидкости (Уравнение Навье –Стокса)
Дифференциальные уравнения движения вязкой жидкости могут быть составлены путем дополнения уравнений Эйлера слагаемыми, определяющими силы сопротивления движению, обусловленные вязкостью жидкости, тогда уравнения Эйлера запишутся в виде
 , (4.25)
, (4.25)
где Fx, Fy, Fz – проекции сил вязкости на координатные оси, отнесенные к единице массы жидкости, т.е. записанные в виде ускорений.
Под действием сил вязкости (сил сопротивления смещению одних частиц жидкости относительно других, смежных с ними) возникают как тангенциальные (касательные), так и нормальные (перпендикулярные) напряжения (напряжения сжатия или растяжения). Определим Fx, Fy, Fz, предполагая, что жидкость движется слоями без перемешивания движущейся массы. В общем случае направление движения не совпадает с направлением координатных осей, вследствие чего не совпадает с направлением этих осей и сила вязкости.
 Выделим элемент жидкости в форме параллелепипеда с ребрами, параллельными координатным осям (рис. 4.4), и определим сумму проекций сил вязкости, действующих только на те три грани параллелепипеда, которые образуют трехгранный угол с вершиной А. Для каждой координатной оси существуют проекции только трех сил (из девяти) отличных от нуля.
Выделим элемент жидкости в форме параллелепипеда с ребрами, параллельными координатным осям (рис. 4.4), и определим сумму проекций сил вязкости, действующих только на те три грани параллелепипеда, которые образуют трехгранный угол с вершиной А. Для каждой координатной оси существуют проекции только трех сил (из девяти) отличных от нуля.
Рис. 4.4
.
Для удобства дальнейших рассуждений введем двойную индексацию напряжений: первый индекс указывает на то, что площадка, для которой определяется напряжение, расположена нормально к данной оси координат, а вторая – направление действия напряжения. Проекции сил, действующих на грани трехгранного угла с вершиной А.
 (4.26)
(4.26)
Переходя к проекциям сил, действующим на грани трехгранного угла с вершиной С’, заметим, что напряжения на этих гранях будут отличаться на величину соответствующих частных дифференциалов этих напряжений
|
|
|
 (4.27)
(4.27)
где для оси ОХ
 (4.28)
(4.28)
Аналогичные выражения можно получить и для двух других осей. Выражение для силы  , представляющей сумму проекций на ось ОХ всех сил вязкости, действующих на массу жидкости в объеме выделенного параллелепипеда, с учетом того, что направление сил, действующих на грани угла с вершиной С, противоположного направлению сил, действующих на грани трехгранного угла с вершиной А, запишется
, представляющей сумму проекций на ось ОХ всех сил вязкости, действующих на массу жидкости в объеме выделенного параллелепипеда, с учетом того, что направление сил, действующих на грани угла с вершиной С, противоположного направлению сил, действующих на грани трехгранного угла с вершиной А, запишется
 (4.29)
(4.29)
С учетом того, что
 (4.30)
(4.30)
имеем
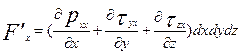 . (4.31)
. (4.31)
Принимая во внимание, что  получим
получим
 (4.32)
(4.32)
Касательные напряжения  в пределах грани dxdz остаются одинаковыми для всех точек этой площадки, т.е. не зависят от координат Х и Z и изменяются только при перемещении этой площадки вдоль оси OY, т.е. зависят от координаты У. Таким образом, касательные напряжения
в пределах грани dxdz остаются одинаковыми для всех точек этой площадки, т.е. не зависят от координат Х и Z и изменяются только при перемещении этой площадки вдоль оси OY, т.е. зависят от координаты У. Таким образом, касательные напряжения  зависят только от градиента скорости
зависят только от градиента скорости  . В соответствии с законом Ньютона имеем
. В соответствии с законом Ньютона имеем
 (4.33)
(4.33)
откуда
 (4.34)
(4.34)
Рассмотрим производную  . Величина
. Величина  представляет собой нормальное к площади dydz напряжение, обусловленное влиянием вязкости (сжатия – в условиях торможения и растяжения – в условиях ускоренного движения) в зависимости от изменения скорости вдоль оси ОХ, т.е. в зависимости от градиента скорости
представляет собой нормальное к площади dydz напряжение, обусловленное влиянием вязкости (сжатия – в условиях торможения и растяжения – в условиях ускоренного движения) в зависимости от изменения скорости вдоль оси ОХ, т.е. в зависимости от градиента скорости  . Поэтому можно допустить, что напряжение
. Поэтому можно допустить, что напряжение  может также определяться по закону Ньютона
может также определяться по закону Ньютона
 (4.35)
(4.35)
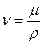
и
 . (4.36)
. (4.36)
Делая соответствующие подстановки, получаем
 . (4.37)
. (4.37)
Аналогично получим
 ; (4.37а)
; (4.37а)
 .
.
В окончательной форме после группировки слагаемых, имеем
 (4.38)
(4.38)
Это и есть уравнения движения вязкой несжимаемой жидкости (уравнения Навье – Стокса).
|
|
|


