 |
Дифференциальные уравнения равновесия жидкости
|
|
|
|
Получим дифференциальные уравнения равновесия жидкости, когда на нее действуют поверхностные силы, определяемые гидростатическим давлением и массовые силы, пропорциональные массе.
Выделим в неподвижной жидкости элементарный объем в форме прямоугольного параллелепипеда с ребрами, параллельными координатным осям и соответственно равными dx, dy, dz.
 |
Рассмотрим условия равновесия выделенного объема жидкости. Пусть внутри параллелепипеда на жидкость действует равнодействующая массовая сила F, составляющие которой, отнесенные к единице массы, равны X, Y, Z.
Рис.2.3. Схема для вывода дифференциальных уравнений равновесия жидкости.
Тогда массовые силы, действующие на выделенный объем в направлении координатных осей, будут равны 
X dxdydz, Ydxdydz, Zdxdydz.
Рассмотрим поверхностные силы. На левую грань параллелепипеда в точке M действует давление р. Давление р есть функция координат x, y, z, но вблизи точки M по всем трем граням оно будет одинаково, что вытекает из свойства гидростатического давления. На противоположную (правую) грань будет действовать давление равное 
(пояснить). 
– градиент давления вблизи точки M в направлении оси X. Таким образом, на левую грань параллелепипеда действует поверхностная сила, равная 
, а на правую 
.
Тогда результирующая поверхностная сила, действующая вдоль оси OX будет
Аналогичным образом определяются поверхностные силы, действующие на грани параллелепипеда в направлении двух других осей.
Тогда уравнения равновесия параллелепипеда в проекциях на координатные оси запишутся в следующем виде
(2.4)
Сокращая на массу 
, получим
(2.5)
Система (2.5) дифференциальных уравнений гидростатики, описывающая условия равновесия жидкости называется уравнениями Эйлера.
|
|
|
Для практического использования удобнее вместо системы уравнений (2.5) получить одно эквивалентное им уравнение, не содержащее частных производных. Для этого умножим первое из уравнений (2.5) на dx, второе – на dy, третье – на dz, и, сложив эти уравнения, получим
.
Трехчлен, заключенный в скобках, представляет собой полный дифференциал давления.
Тогда предыдущее уравнение можно записать в виде
.
или
- (2.6)
основное уравнение гидростатики в дифференциальном виде.
2.4 Равновесие жидкости в поле силы тяжести. Поверхность уровня
В случае равновесия жидкости в поле земного тяготения на жидкость действует только сила тяжести, т.е.
X=Y=0, Z=-g.
Тогда основное дифференциальное уравнение статики (2.6) запишется в виде
. (2.7)
После интегрирования будем иметь
. (2.8)
Для определения постоянной интегрирования C рассмотрим резервуар, наполненный жидкостью, (Рис.2.4), со свободной поверхностью. Для точки лежащей на поверхности z=zo, р=рo. Подставив эти значения в уравнение (2.8), получим
C=рo+ 
gzo.
Рис.2.4. схема для вывода основного уравнения гидростатики.
Тогда уравнение (2.8) запишется 
или 
- (2.9)
основное уравнение гидростатики; по нему можно подсчитать давление в любой точке покоящейся жидкости.
Или
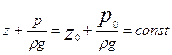. (2.9а)
Принимая во внимание, что разность z-zo=h, а 
- удельный вес, уравнение (2.9) можно переписать в виде
или 
, (2.10)
где h- глубина погружения точки М.
Величины z и 
в гидростатике называют соответственно геометрической и пьезометрической высотой.
Сумма 
называется гидростатическим напором. Из уравнения (2.9а) видно, что гидростатический напор есть величина постоянная для всего объема неподвижной жидкости.
Согласно уравнению (2.10) давление в любой точке покоящейся жидкости складывается из двух величин: давления р0 на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.
|
|
|
Величина р0 является одинаковой для всех точек объема жидкости, поэтому, учитывая свойство гидростатического давления, можно сказать, что давление, приложенное к внешней поверхности жидкости передается всем точкам этой жидкости и по всем направлениям одинаково – закон Паскаля.
Давление жидкости, как видно из формулы (2.10), возрастает с увеличением глубины по линейному закону и на данной глубине есть величина постоянная (см. рис 2.5).
Рис. 2.5. Распределение давления
а – распределение полного гидростатического давления.
б – распределение избыточного гидростатического давления.
Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня. В данном случае поверхностями уровня являются горизонтальные плоскости (свободная поверхность – одна из них).
Уравнение поверхности равного давления легко можно получить из основного дифференциального уравнения гидростатики (2.6), так как на поверхности уровня p=const в любой ее точке, dp=0 и, следовательно правая часть уравнения тоже равна нулю. Поскольку 
0, тогда
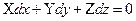- (2.11).
уравнение поверхности уровня.
Относительное равновесие.
Ранее было рассмотрено равновесие жидкости под действием лишь одной массовой силы – силы веса жидкости. Этот случай имеет место тогда, когда жидкость покоится в неподвижном сосуде или сосуде, движущемся прямолинейно и равномерно. Если же сосуд с жидкостью находится в неравномерном или непрямолинейном движении, то на частицы жидкости кроме силы тяжести действуют еще силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем (равновесием).
При рассмотрении относительного равновесия обычно решаются две задачи: определяется форма поверхности уровня (равного давления) и выясняется характер распределения давления. Эти задачи решаются с помощью уже известных уравнений (2.6) и (2.11).
2.5.1. Движение резервуара с жидкостью по вертикали с постоянным ускорением а (рис.2.6).
Для определения формы поверхности равного давления воспользуемся уравнением (2.11). Проекции единичных массовых сил на координатные оси будут: 
. Знак «-»-равноускоренный подъем, «+»-спуск.
|
|
|
Рис.2.6. Вертикальное перемещение резервуара с жидкостью.
Составим уравнение поверхности уровня
(-g. 
. (2.12)
Если 
, то dz=0 и, следовательно, z=const, т.е.поверхности равного давления представляют собой горизонтальные плоскости. (При спуске и а=g 
невесомость).
Характер распределения давления в рассматриваемом случае получим из основного уравнения равновесия жидкости (2.6), которое принимает форму:
Интегрируя, получим
,
где С – постоянная интегрирования, определяемая из граничных условий поверхности z=z0, p=p0.
После подстановки граничных условий, получаем закон распределения давления вдоль любой вертикали:
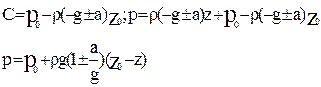(2.13)
2.5.2. Вращение цилиндрического сосуда с жидкостью с постоянной угловой скоростью 
. (рис.2.7)
Определим форму свободной поверхности (поверхности уровня) и закон распределения давления. Выберем вблизи свободной поверхности частицу жидкости массой dm; на эту частицу действует массовая сила dF, направленная по нормали к свободной поверхности. (это свойство поверхности уровня: равнодействующая массовых сил всегда направлена по нормали к поверхности уровня)
Рис. 2.7. Вращение
резервуара с жидкостью.
Разложим эту силу на две составляющие: горизонтальную (центробежную) силу dFr=dm 
2r и вертикальную, определяемую полем силы тяжести dFg=-dmg.
Разделив действующие силы на dm, получим:
X= 2rcos 
= 2x;
Y= 2rsin = 2y;
Z=-g.
Дифференциальное уравнение поверхности уровня в этом случае будет
2xdx+ 2ydy-gdz=0 или 2rdr-gdz=0. (2.14)
Интегрируя уравнение (2.14), получим для поверхности равного давления
. (2.15)
Таким образом, поверхностью равного давления будет семейство параболоидов вращения, осью симметрии которых является ось OZ.
Закон распределения давления найдем из дифференциального уравнения (2.6), которое в данном случае примет вид
(2.16)
После интегрирования с учетом граничных условий (r=0, z=zo, р=р0) получим закон распределения давления:
, (2.17)
(здесь уже найдена постоянная интегрирования С)
|
|
|
Это значит, что давление возрастает пропорционально радиусу и уменьшается пропорционально высоте z. (пропорционально r возрастает инерционная составляющая массовой силы, а с увеличением r массовая сила уменьшается, т.к. результирующая массовая сила всегда нормальна к поверхности уровня – угол наклона вектора массовой силы увеличивается. (см.рис.).
|
|
|
