 |
Гидравлические сопротивления
|
|
|
|
Виды гидравлических сопротивлений
При движении жидкости по трубе между нею и стенками трубы возникают дополнительные силы сопротивления, в результате чего частицы жидкости, прилегающие к поверхности трубы, тормозятся. Это торможение вследствие вязкости жидкости передается следующим слоям.
Равнодействующая сил сопротивления T направлена против движения (рис.5.1). Это и есть силы гидравлического трения (гидравлического сопротивления трения). Необходимые для преодоления сил сопротивления энергию или напор называют потерянной энергией или потерями напора.
Рис.5.1
Потери напора, затрачиваемые на преодоление сопротивления трения, носят название потерь напора на трение по длине (линейные потери напора) и обозначают hтр.
Однако потери напора, возникающие при движении жидкости, зависят не только от трения о стенки.
Рассмотрим другой пример. Бак объемом W (рис.5.2) наполнен водой при постоянном уровне H и питает горизонтальную трубу АВ длиной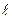 
одинакового по всей длине диаметра d. Пусть расход воды равен Q. Если трубу АВ заменить трубой CD той же длины 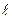, но образованной из последовательно расположенных участков диаметрами d и 2d, то расход изменится. Новый расход 
<Q (иногда =0,5Q и даже <).
Рис. 5.2.
Таким образом, резкие изменения сечения также оказывают сопротивление движению жидкости и вызывают потери энергии (напора). Существуют и другие причины, вызывающие потери напора: внезапное сужение, расширение, изменение направления движения жидкости и т.п.
Потери напора, вызываемые резким изменением конфигурации границ потока, называют местными потерями напора или потерями напора на местные сопротивления и обозначают hм.
|
|
|
Следовательно, потери напора при движении жидкости складываются из потерь напора на трение и потерь напора на местные сопротивления, т.е.
hн=hтр+hм. (5.1)
Определение потерь напора при движении жидкости является одной из важнейших задач гидравлики.
Потери напора на трение hтр при движении жидкости по трубам могут зависеть от следующих факторов:
- диаметра трубы d и ее длины ;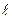
- физических свойств жидкости (плотности 
и вязкости 
);
- средней скорости жидкости в трубе 
;
- средней высоты выступов поверхности на стенках трубы.
Для определения потерь на трение пользуются формулой Дарси – Вейсбаха
. (5.2)
Из формулы (5.2) следует, что потеря напора на трение по длине возрастает с увеличением средней скорости потока и длины рассматриваемого участка трубы и обратно пропорциональна ее диаметру. Неизвестный безразмерный коэффициент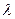 
называется коэффициентом гидравлического трения (к – т Дарси). Определение его численных значений для различных конкретных случаев течения жидкости будет дано позже.
Формула для определения потерь напора на местное сопротивление имеет вид:
, (5.3)
где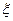 
- безразмерный коэффициент, или коэффициент местных потерь;
- скорость потока после перехода через местное сопротивление.
Режимы течения жидкости в трубах.
Число Рейнольдса
Наблюдения показывают, что в природе существуют два различных вида (режима) течения жидкости:
1) слоистое упорядоченное, или ламинарное течение, при котором отдельные слои жидкости скользят относительно друг друга, не смешиваясь между собой;
2) неупорядоченное, или турбулентное, течение, когда частицы жидкости движутся по сложным, все время изменяющимся траекториям и в жидкости происходит интенсивное перемешивание.
Указанные течения жидкости можно наблюдать на приборе, представленном на рис. 5.3. Пояснить опыт.
При малых скоростях движения воды в трубе окрашенная струйка не размывается окружающей ее водой (ламинарный поток). При увеличении скорости движения воды окрашенные струйки получают вначале волнистое очертание (начинают колебаться), а затем почти внезапно исчезают, размываясь по всему объему трубы и окрашивая всю жидкость – турбулентное движение.
|
|
|
Рис.5.3. Схема прибора для демонстрации режимов течения.
Таким образом при ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, т.е. прямолинейно, при этом отсутствуют поперечные перемещения жидкости.
При турбулентном течении векторы скоростей имеют не только осевые, но и нормальные к оси трубы, составляющие, поэтому наряду с основным продольным перемещением жидкости вдоль трубы происходят поперечные перемещения (перемешивание) и вращательное движение отдельных объемов жидкости. Этим и объясняются пульсации скоростей и давления в потоке.
Переход от ламинарного течения к турбулентному происходит при определенной скорости (так называемой критической скорости), которая для труб разных диаметров оказывается различной, возрастающей с увеличением вязкости и снижающейся с уменьшением диаметра трубы.
Осборн Рейнольдс установил общие условия, при которых возможны существование ламинарного и турбулентного режимов движения жидкости и переход от одного режима к другому.
Оказалось, что режим потока жидкости в трубе зависит от безразмерного числа, которое учитывает основные факторы определяющие это движение: среднюю скорость , диаметр трубы d и вязкость жидкости 
. Это число называется числом Рейпольдса и имеет вид
. (5.4)
Диаметр d в числе Re может быть заменен на любой линейный размер (диаметр шара, длина крыла самолета и т.п.)
Число Re, при котором происходит переход от ламинарного режима течения к турбулентному, называют критическим и обозначают Reкр (а соответствующую ему скорость называют критической скоростью)
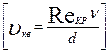
Как показывают опыты для труб круглого сечения Reкр 
2300( 2000)
При Re<Reкр течение является ламинарным, при Re>Reкр – турбулентным. Точнее говоря, развитое турбулентное течение в трубах устанавливается
лишь при Re 4000, а при Re =2300 
4000 имеет место переходная критическая область.
|
|
|
Зная скорость движения жидкости, и ее вязкость и диаметр трубы, можно найти число Re и, сравнив его с Reкр, определить режим течения жидкости.
На практике имеют место как ламинарное, так и турбулентное течения, причем первое наблюдается в основном в тех случаях, когда по трубам движутся вязкие жидкости (смазочные масла), второе обычно там, где по тубам перетекают маловязкие жидкости (вода, бензин, спирт, газы).
Значение чисел Re:
- газопроводы сети домового потребления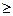 
3000;
- городские сети 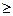200000;
- вентиляционные сети 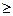150000;
- сети сжатого воздуха 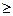400000;
- паропроводы центрального отопления 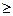30000
При ламинарном течении в трубе распределение скоростей по сечению имеет параболический характер: непосредственно у стенок скорости равны нулю, а при удалении от них непрерывно и плавно возрастают, достигая максимума на оси трубы (рис. 5.4).
При турбулентном движении закон распределения скоростей сложнее: в большей части поперечного сечения скорости лишь незначительно меньше максимального значения (на оси), но зато вблизи стенок величина скорости резко падает (рис. 5.5) в пределах очень тонкого слоя.
Рис. 5.4. Распределение Рис.5.5. Распределение
скоростей при ламинарном движении скоростей при турбулент -
жидкости в трубах. ном движении жидкости
в трубах.
1-вязкий подслой;
2-ядро потока
|
|
|
