 |
Общие сведения. Простой трубопровод постоянного сечения
|
|
|
|
При гидравлическом расчете трубопроводы подразделяют на простые и сложные.
Простым называют трубопровод, состоящий из одной линии труб (не имеет ответвлений) с постоянным расходом по длине трубопровода.
Всякие другие трубопроводы называются сложными.
 |
Рассмотрим простой трубопровод постоянного сечения. При истечении в атмосферу (рис. 6.1а),
Рис.6.1. К расчету простого трубопровода
уравнение Бернулли, записанное для сечений на поверхности воды в резервуаре и на выходы из трубы, имеет вид:
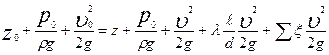
Пренебрегая величиной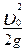 
(очень малой по сравнению с другими членами уравнения) и обозначая z0-z=H, приводим уравнение Бернулли к виду:
. (6.1)
При истечении под уровень (рис. 6.1б) получим аналогично:
.
В этом уравнении в отличие от предыдущего местные сопротивления оценены двумя слагаемыми 
и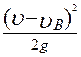 
. Первое слагаемое так же, как и в предыдущем случае, учитывает потери напора на протяжении трубопровода, начиная от выхода из резервуара А в трубу (точка а) и до конца трубы (точка б), за исключением потерь напора на выход в резервуаре В, которые оценены вторым слагаемым.
По аналогии с первым случаем, пренебрегая величино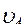й 
и 
, можно привести и это уравнение к виду:
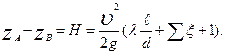(6.2)
Формулы (6.1) и (6.2) тождественны между собой, и гидравлические расчеты для обеих схем трубопровода будут одинаковы.
Различие состоит лишь в том, что при истечении под уровень, единица, стоящая в скобках в правой части, представляет собой коэффициент сопротивления «на выход» потока под уровень, в то время как при истечении в атмосферу она учитывает кинетическую энергию, оставшуюся в потоке после выхода из трубопровода, которая может быть так или иначе использована.
|
|
|
Таким образом, напор Н при истечении под уровень равен сумме всех сопротивлений: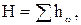 
при истечении же в атмосферу он делится на две части: кинетическую энергию, уносимую потоком из трубы, и сумму потерь напора
.
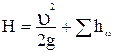Гидравлический расчет простого трубопровода сводится к решения трех основных задач (для заданных конфигураций трубопровода, его материала и длины).
Первая задача. Требуется определить напор Н, необходимый для пропуска заданного расхода жидкости Q по заданному трубопроводу диаметром d и длиной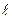 
(шероховатость известна). Задача решается путем непосредственного использования формулы (6.1) с предварительным вычислением средней скорости
.
Тогда искомый напор
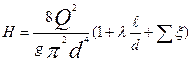(6.3)
Определение значений коэффициентов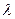 
и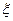 
в данной задаче не вызывает затруднений, они находятся на основании известного числа Re (легко находится) и относительной шероховатости трубопровода.
Вторая задача. Требуется определить пропускную способность (расход) трубопровода Q при условии, что известны напор Н, длина трубы 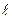и ее диаметр d (и шероховатость). Задача решается с помощью формулы (6.3), согласно которой
. (6.4)
Т.к. коэффициенты 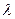и 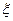являются функциями числа Re, которое связано с неизвестным и искомым здесь расходом Q, то решение находим методом последовательных приближений, полагая в первом приближении существование квадратичного закона сопротивления, при котором коэффициенты 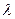и 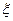не зависят от числа Re (а определяются только относительной шероховатостью стенок трубопроводов).
Третья задача. Требуется определить диаметр трубопровода d при заданных значениях Q, 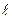и Н. Здесь также используем формулу (6.4), но встречаемся с трудностями в вычислениях вследствие того, что Re неизвестно, неизвестна следовательно и 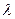. Решение задачи производится также методом последовательных приближений, полагая в первом приближении наличие квадратичного закона сопротивления, при котором коэффициент 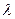является функцией только диаметра (при заданной шероховатости стенок трубы)
|
|
|
Тогда уравнение (6.4) приводится к виду
.
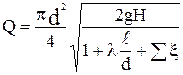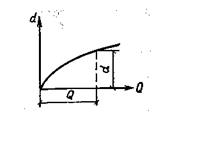
Задаваясь рядом значений диаметра d1, d2, …,du и вычисляя по последней формуле соответственно Q1, Q2, …, Qu, строим график Q=f(d) (рис.6.2), из которого определяем диаметр, отвечающий заданному расходу.
Рис.6.2. К расчету диаметра
Трубопровода при заданном
расходе
6.1.1. Рассмотрим простой трубопровод, состоящий из труб разного диаметра (рис. 6.3), уложенных в одну линию одна вслед за другой (последовательное соединение труб). Уравнение Бернулли для этого случая запишется в виде:
,
где 
- потери напора на первом, втором и т.д. участках трубопровода.
Рис.6.3. Последовательное соединение трубопроводов
Потери напора на первом участке с диаметром трубы d1:
Аналогично для последующих участков:
В последнем равенстве в скобках добавлено третье слагаемое – единица, учитывающая потери напора на выход (об этом говорилось ранее)
Таким образом, расчетное уравнение имеет вид:
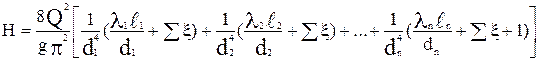. (6.5)
Из уравнения (6.5) видно, что решение первой и второй задач будет таким же, как для трубопровода постоянного диаметра.
Третья же задача, если в ней есть потребность определения всех диаметров для всех участков, становится неопределенной, т.к. в этом случае уравнение (6.5) содержало бы n неизвестных. Очевидно, что для определенности решения надо задавать диаметры труб для всех участков, кроме одного.
6.1.2. Расчет длинных трубопроводов в квадратичной областисопротивления.
Квадратичная область сопротивления – когда коэффициент гидравлического трения не зависит от числа Re, а определяется только относительной шероховатостью стенок трубопровода.
В длинных трубопроводах потери напора на трение во много раз превосходят потери на местные сопротивления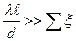 
и скоростной напор на выходе, поэтому последними часто пренебрегают.
Например, в магистральных водопроводах местные потери напора часто составляют < 2-3% от потерь на трение.
Для длинных трубопроводов уравнения (6.1)и (6.2) принимают вид:
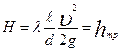. (6.6)
Уравнение (6.3) приводится к виду
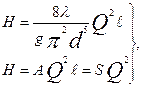(6.7)
Уравнение (6.4) к виду
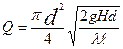или 
, (6.8)
где А – удельное сопротивление трубопровода
. (6.9)
|
|
|
А полное сопротивление
S=A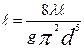 
. (6.10)
Если обозначить
, (6.11)
то уравнение (6.7) примет вид
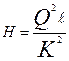. (6.12)
Показатель К, имеющий размерность расхода, называется модулем расхода или расходной характеристикой трубопровода.
Показатели A, S,K представляют собой обобщенные гидравлические параметры трубопровода, использование которых значительно упрощает гидравлические расчеты.
Действительно, для квадратичной области сопротивления параметры Акв и Ккв зависят только от диаметра трубопровода (при заданной его шероховатости), а параметр Sкв – от диаметра и длинны трубопровода. Следовательно, значения обобщенных гидравлических параметров могут быть заранее вычислены для каждого диаметра d, входящего в установленный стандарт и сведены в таблицы. Так, например, в таблице 6.1 [1] приведены значения Акв, подсчитанные по формуле (6.9) при значении Кэ=0,1мм.
Три основные задачи по расчету трубопроводов с использованием обобщенных гидравлических параметров решаются следующим образом:
1) определение напора Н, необходимого для пропуска расхода Q по заданному трубопроводу диаметром d, производится непосредственно по формуле (6.7) или (6.12);
2) для определения пропускной способности трубы Q при заданных d, 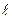,H предварительно находится из таблиц Акв или Ккв, после чего используется формула (6.8) или (6.12);
3) для определения необходимого диаметра d при заданных Q, 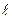,H предварительно из формул (6.7) или (6.12) находится значение Акв (или Ккв), по которому из таблиц находим d.
При последовательном соединении трубопроводов различных диаметров и длины полная потеря напора в трубопроводе будет
.
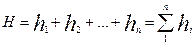Подставляя для каждой потери напора ее выражения по формуле (6.7), получим
, (6.13)
где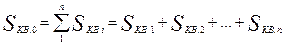 
(6.14)
Таким образом, при последовательном соединении трубопроводов сопротивления отдельных участков складываются.
Из уравнения (6.13) находим выражение для пропускаемого расхода
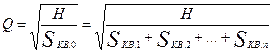. (6.15)
По найденному расходу можно вычислить потери напора на отдельных участках (например,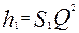 
, и т.д.) и построить кривую давления (пьезометрическую линию), которая будет иметь вид ломаной линии.
|
|
|
В случае неквадратичной области сопротивления параметры А (или К) зависят не только от диаметра трубы, но также и от скорости движения в ней, в связи с чем решение задач несколько осложняется.
Формулу (6.7) можно представить в виде
. (6.16)
Введем обозначение 
, где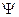 
- поправка на неквадратичность.
Тогда формула (6.16) примет вид
, (6.17)
где 
- формулы Альтшуля А.Д.
Принимая во внимание выражения для 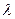и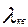 
, получим
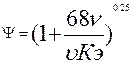. (6.18)
.
|
|
|
