Уравнение неразрывности сжимаемой жидкости.

При рассмотрении движения сжимаемой жидкости будем предполагать, что движущая жидкость сплошь заполняет все пространство, т.е. пустоты или разрывы не образуются. Это условие называется условием неразрывности или сплошности движения.

В таком случае, рассматривая протекание жидкости через некоторую фиксированную в пространстве замкнутую поверхность, можно заключить, что в случае несжимаемой жидкости количество вытекшей жидкости вследствие условия неразрывности должно в точности равняться количеству втекшей жидкости. Если же за некоторый промежуток времени количество вытекшей жидкости будет превышать количество втекшей, то внутри этой поверхности произойдет изменение плотности. Сказанное выше можно представить в виде дифференциального уравнения, носящего название уравнения неразрывности или сплошности движения.

Уравнение неразрывности в газовой динамике является выражением закона сохранения материи, установленного впервые великим русским ученым М.В.Ломоносовым в 1748 году.

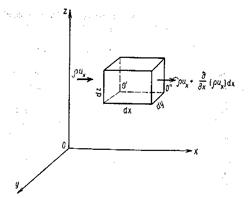
Рассмотрим фиксированную в пространстве замкнутую поверхность, имеющую форму прямоугольного параллелепипеда с ребрами d_x d_y d_z, через который протекает сжимаемая жидкость.

Пусть в единицу времени и через единицу площади левой грани параллелепипеда в направлении оси Х протекает масса жидкости u_x.

Рис.3.3.К выводу уравнения неразрывности.

 

Так как u_x есть функция координат и времени, т.е. u_x=f(x, y, z, t), то для определения массы жидкости, протекающей в направлении оси Х в единицу времени через единицу площади правой грани, надо координате Х в функции f(x, y, z, t) дать приращение d_x, т.е. надо найти f(x+ d_x, y, z, t). Но с точностью до малых первого порядка

f(x+ d_x, y, z, t)= f(x, y, z, t)+ ,

а через единицу площади правой грани в единицу времени протекает в направлении оси Х масса жидкости, равная

.

Очевидно, разность между вытекшим и втекшим количеством жидкости будет

,

и, следовательно за время dt через грани площадью d_yd_z вытечет в направлении оси Х масса жидкости

.

Аналогично разности между вытекшим и втекшим количеством жидкости в направлении осей Y и Z за время dt можно получить в виде

 

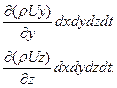
Если эти выражения сложить, то получим суммарную разность между всей вытекшей и втекшей за время dt жидкостью:

Различие в количествах (массе) вытекшей и втекшей жидкости отразится на количестве жидкости внутри параллелепипеда. В самом деле, если в момент времени t плотность была , то в момент t+dt плотность будет равна

и, следовательно, за время dt количество (масса) жидкости внутри параллелепипеда изменится от величины до

т.е. на величину

(здесь берем знак минус, т.к.

раньше подсчитывалась разность

между вытекшим и втекшим коли-

чествами).

В силу условия неразрывности разность между количествами вытекшей и втекшей жидкости должна быть равна изменению количества жидкости внутри параллелепипеда. Поэтому, приравнивая соответствущие выражения, получаем

или

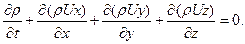(3.5)

Это уравнение носит название дифференциального уравнения неразрывности для сжимаемой жидкости.

 

 

Если движение сжимаемой жидкости установившееся, то, очевидно

и уравнение неразрывности примет вид

(3.6)

Уравнения неразрывности (3.5) и (3.6) часто записывают в несколько иной форме. Получим ее. Для этого выполним дифференцирование в уравнении(3.5)

Замечая, что первые четыре слагаемых представляют собой полную производную от по времени t, получим уравнение неразрывности в иной форме:

(3.7)

В частном случае, когда жидкость несжимаемая, т.е. =const уравнение неразрывности примет вид

или divU=0 (3.8)

Это уравнение неразрывности для несжимаемой жидкости.

Уравнение неразрывности часто используется в интегральной форме (уравнение расхода). Для его вывода рассмотрим элемент трубки тока, расположенный между произвольно проведенными контрольными сечениями.

Согласно закону сохранения массы при стационарном течении количество жидкости, втекающей внутрь рассматриваемого объема при отсутствии внутренних источников, должно равняться количеству жидкости, покидающей этот объем. Другими словами, расход массы жидкости через поверхность рассматриваемого объема должен быть равен нулю:

(3.9)

Рис. 3.4. Течение жидкости в трубке тока.

 

При установившемся движении можно записать

 

Здесь F – площадь всей поверхности рассматриваемого объема;

Un – скорость жидкости в каждой точке, нормальная к элементу поверхности dF.

 

 

Движение жидкой частицы

Рассмотрим движение бесконечно малой жидкой частицы, имеющей первоначальную форму параллелепипеда (рис.3.5)

 

 

Рис.3.5

 

 

В отличие от твердого тела жидкая частица при своем движении может сильно деформироваться.

Грани этой частицы, имеющей в начале движения форму прямого параллелепипеда с ребрами dx, dy, dz, с течением времени могут скашиваться и растягиваться (рис.3.6, 3.7)

 

 

 

 

 

 

Рис.3.6. Угловая деформация граней Рис. 3.7. Линейная деформация граней.

 

Пусть составляющие скорости движения частицы в точке (рис.3.5) суть Ux, Uy, Uz, тогда составляющие скорости в точке b равны

в точке d

и в точке е

Скашивание ребра ab частицы за бесконечно малое время dt, которое вызывается разностью компонентов скорости в точках и b (рис.3.6), характеризуется смещением точки b, равным

Относительное смещение или угловая деформация

Скашивание ребра приводит к угловой деформации

Ввиду того, что угловые деформации за время dt незначительны, угол наклона грани можно считать равным тангенсу этого угла. Полное скашивание прямого угла в точке в этом случае равно

а скорость соответствующей угловой деформации

. (3.10а)

Индекс z указывает на то, что рассматривается деформация частицы в плоскости XУ, перпендикулярной к оси Z; в остальных двух плоскостях скорости скашивания координатных углов равны, очевидно,

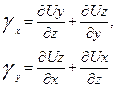
(3.10б)

(3.10в)

Используя те же угловые смещения граней частицы, можно определить угловые скорости ее вращения. Поскольку направления вращения ребер b и ad противоположны, средняя угловая скорость вращения частицы в целом около оси Z составляет

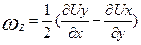. (3.11а)

Для остальных двух осей вращения имеем соответственно

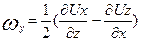, . (3.11б)

Вектор угловой скорости вращения , составляющие которого суть 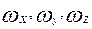, носит название завихренности, или вихря скорости. Его величина определяется следующим равенством:

. (3.12)

 

Динамика жидкости

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: