Перемещения при изгибе балок

Дифференциальное уравнение изогнутой оси упру­гой балки

При расчете балок на изгиб инженер интересуется не только напряже­ниями, возникающими от действия внешних сил, но и перемещениями от действия тех же сил. Одно из требований к элементам конструкций, чтобы перемещение не превосходило некоторого допусти­мого значения, обусловленного требованиями эксплуатации. Это условие называется условием жесткости либо конструктивной прочности.

При расчете строительных и машиностроительных конструкций на жесткость (в большинстве случаев по прогибам, по углам поворота) должно соблюдаться условие

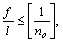
т.е. относительный прогиб f/l, подсчитанный при действии нормативных нагрузок, не должен превышать установленный нормами предельный прогиб 1/ n_o для данного вида конструкции.

Для обеспечения нормальной работы подшипников скольжения и роликовых подшипников качения иногда ставится дополнительное условие жесткости – ограничение угла поворота опорных сечений:

.

Допускаемый угол поворота берется из соответствующих справочников. В среднем составляет 0,001 рад.

Рассмотрим плоский чистый изгиб балки (рис. 6.41, а).

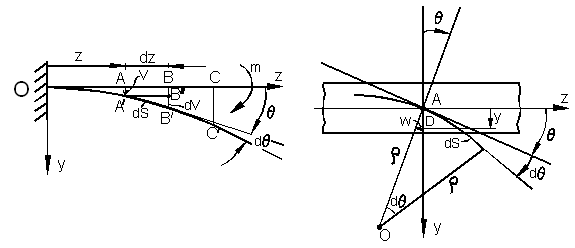
А) б)

Рис. 6.41

 

В результате действия изгибающего момента m ось балки ОС изгибается и занимает некоторое положение ОС'. Произвольная точка А оси балки, характе­ризуемая координатой 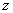, перемещается в новое положение А '. Перемещение, изображаемое направленным отрезком , назовем прогибом балки для точки А с координатой 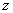и обозначим v. Проведем в точке А ' касательную к изогнутой оси балки. Она образует с осью 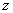угол .

Из рис. 6.41, б видно, что этот угол в силу взаимной перпендикулярности сто­рон в точности равен углу поворота поперечного сечения. При изменении 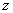, т.е. при переходе к другим точкам оси балки, прогиб v и угол поворота поперечного сечения изменяется. Следовательно, они являются функциями :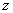

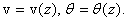(19)

Горизонтальное перемещение w произвольной точки D поперечного се­чения на расстоянии от оси балки равно:

(20)

Из треугольника А'В'В" следует, что первая производная от функции прогиба :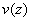

(21)

равна тангенсу угла наклона касательной к изогнутой оси балки в точке А с координатой 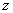. Из этого же треугольника получаем

(22)

Из рис. 6.41, б находим где - радиус кривизны дуги . Следовательно, кривизна изогнутой оси в точке А равна:

(23)

Дифференцируя (21) по 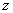и учитывая (19), (22), (23), получаем:

откуда

(24)

Формула для кривизны балки

для положительных значений 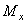. В нашем примере на рис. 6.41 изгибающий момент . Поэтому эту формулу мы должны использовать в виде:

(25)

Приравнивая (24), (25), получаем точное дифференциальное уравнение изогнутой оси балки:

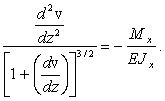(26)

Если прогибы балки малы по сравнению с ее линейными размерами, то и углы поворота сечений - малые величины и, согласно (21)-(24), можно считать:

, ,

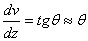Тогда дифференциальное уравнение (26) упрощается и принимает вид

(27)

Уравнение (27) носит название приближенного дифференциального уравнения изогнутой оси упругой балки. Оно получено для случая чи­стого изгиба, но может быть использовано и при поперечном, когда мо­мент является функцией .

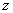Интегрируя (27), получаем:

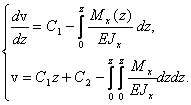(28)

Произвольные постоянные C ₁, С ₂ в (28) имеют простой геометрический смысл. Обозначим через прогиб и угол поворота cечения соответственно в начале координат при . Тогда при из (10) получаем:

Величины называют начальными параметрами задачи по определению перемещений в балках.

Соотношения (28) запишем в виде

(29)

Так как

то решение (29) можно записать в виде:

В соответствии с дифференциальными зависимостями Журавского

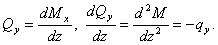(30)

Дифференцируя (27) дважды по 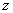и используя зависимости (30), находим

(31)

. (32)

При постоянной жесткости получаем

(33)

(34)

Уравнения (32), (34) представляют собой вторую форму дифферен­циальных уравнений изогнутой оси балки четвертого порядка.

Общее решение неоднородного уравнения (34) имеет вид

(35)

где 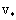- его частное решение. Постоянные находятся из условий на опорах балки. Эти условия называют граничными или краевыми.

Рассмотрим типичные условия закрепления или опирания балок (рис. 6.42). Изогнутая ось балки изображена тонкой линией.

А) б) в)

Рис. 6.42

 

а) Край балки жестко защемлен (рис. 6.42, а). При z = 0 на защемленном крае прогиб и угол поворота сечения равны нулю, т.е.

б) Край балки свободен от закрепления и нагрузки (рис.6.42, а). В этом случае при равны нулю: момент и перерезывающая сила:

в) Край балки шарнирно закреплен либо свободно опёрт (рис. 6.42, б). При z = 0 край балки шарнирно закреплен. Здесь прогиб и момент 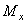равны нулю, т.е.

При балка свободно лежит на опоре. Прогиб равен нулю, но изгибающий момент в сечении балки отличен от нуля. Поэтому здесь только одно граничное условие .

г) Незакрепленный край балки с действующими сосредоточенными силой и моментом (рис. 6.42, в).

В этом случае при имеем статические граничные условия:

 

Пределы применимости приближенной теории из­гиба балок

При выводе дифференциального уравнения изогнутой оси балки (28) выражение для кривизны балки было выбрано приближенно. Выясним степень точности приближенного уравнения (27). Для этого рассмотрим задачу о чистом изгибе консольной балки (рис. 6.43).

Рис. 6.43

 

В этом случае и поэтому Из рис. 6.43 прогиб на конце консоли:

Разложим косинус в ряд и ограничимся тремя первыми элементами:

Выражение для прогиба f принимает вид:

или с учетом и (7):

(36)

Дадим теперь приближенное решение задачи. Интегрируя уравнение

при 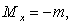получаем:

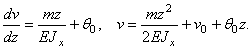
Так как при прогиб , угол поворота , то

При на конце консоли прогиб:

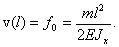(37)

Сравнивая решения (36), (37), находим:

Удовлетворимся при определении прогибов по приближенной теории точ­ностью в 3%. Полагая

получаем:

Таким образом, приближенное дифференциальное уравнение (27) изо­гнутой оси упругой балки дает достаточную точность решения задачи даже в том случае, когда прогиб составляет 30% от длины стержня. Та­кие прогибы возможны только у очень гибких балок большой длины или очень малой толщины типа гибкой стальной линейки.

Вопросы для самопроверки

- Что называется балкой?

- Какой вид нагружения называется изгибом?

- Какой изгиб называется чистым, поперечным?

- Какой изгиб называют чистым, поперечным, прямым и косым?

- Чем отличается чистый изгиб от поперечного изгиба, прямой изгиб от косого изгиба?

- Сформулируйте определение «поперечный изгиб»?

- Сформулируйте понятие «чистый изгиб»?

- Какую плоскость называют силовой?

- Что понимается под волокнами бруса? В чем сущность гипотезы плоских сечений и допущения о ненадавливании волокон друг на друга?

- Что такое нейтральная линия, силовая линия?

- Докажите, что при прямом изгибе нейтральная линия является центральной главной осью поперечного сечения бруса?

- Какие силовые факторы возникают в сечении балки при чистом изгибе?

- Какие силовые факторы возникают в сечении при поперечном изгибе?

- Какой силовой фактор вызывает изгиб бруса? Охарактеризуйте тип деформации бруса при изгибе? Что такое нейтральный слой?

- Что такое изгибающий момент (M _х)? Выразите M _х через напряжения в рассматриваемом сечении? Как определя­ется M _х через внешние силы?

- Что такое поперечная сила (Q _y)? Как определяется Q _y через внешние силы?

- Чем отличается статически определимая балка от статически неопределимой?

- Для чего в многопролетных балках вводятся промежуточные шарниры?

- Какие виды нагрузок могут действовать на балку?

- Какие виды опор встречаются при расчете балок? Чем они отличаются?

- Что подразумевается под понятием «поперечная сила»? как она определяется?

- Какое правило законов для определения поперечной силы используется?

- Сформулируйте определения понятия «изгибающий момент, действующий в сечении балки»?

- Каково правило законов для определения изгибающего момента используется?

- Как вычисляется изгибающий момент в поперечном сечении балки?

- Как вычисляются поперечная и продольная силы в поперечном сечении балки?

- Как определить значение поперечной силы и изгибающего момента в произвольном сечении балки?

- Как определить знаки поперечной силы и изгибающего момента?

- Какие уравнения используются для определения значений опорных реакций?

- Как проверить правильность определения опорных реакций?

- Как формулируется гипотеза плоских сечений?

- Что представляют собой нейтральный слой и нейтральная линия и как они расположены?

- По какой формуле определяются нормальные напряжения в поперечном сечении балки при чистом изгибе и как они изменяются по высоте балки?

- Что называется моментом сопротивления при изгибе и какова его размерность?

- Для чего строят эпюры внутренних силовых факторов?

- Как можно контролировать построение эпюр поперечных сил Q и изгибающих моментов М?

- Опишите особенности очертания эпюр M _х и Q _y: в каких сечениях наблюдаются скачкообразные изменения орди­нат в эпюре M _х; на каких участках эпюра M _х — линейная функция, a Q _y = const, почему в местах приложения попереч­ной сосредоточенной силы в эпюре Q _y — скачок, а в эпюре M _х — «излом» направления касательной; почему в сечениях, в которых M _х имеет экстремальные значения, Q _y = 0 или про­скакивает через нулевое значение?

- Если эпюра поперечной силы ограничена наклонной прямой, как выглядит эпюра изгибающего момента?

- Как определить положение экстремального значения изгибающего момента при действии распределенной нагрузки на участке балки?

- Распределенная нагрузка направлена вверх. Как выглядит парабола, очерчивающая эпюру изгибающих моментов вдоль оси бруса?

- Какой линей очерчена эпюра изгибающих моментов, если закон их изменения по длине балки выражается уравнением: ?

- Как находят опасные сечения?

- Какими зависимостями связаны изгибающий момент, поперечная сила и интенсивность распределенной нагрузки? Как эти зависимости используют при проверке правильности построения эпюр поперечных сил и изгибающих моментов?

- Получите дифференциальные зависимости между изгибающим моментом (M _х), поперечной силой (Q _y) и интен­сивностью внешней нагрузки q?

- В какой последовательности строят эпюры поперечных сил и изгибающих моментов?

- Почему для определения значения поперечной силы и изгибающего момента в произвольном сечении балки на двух опорах необходимо знать реакции опор?

- Как изменяется поперечная сила в сечении балки, к которому приложена сосредоточенная сила? Как изменяется значение изгибающего момента в сечении балки, к которому приложен сосредоточенный момент?

- Как определить максимум и минимум эпюры изгибающих моментов?

- Какие допущения положены в основу вывода формулы для определения нормальных напряжений при изгибе?

- Получите соотношение между величиной изгибающего момента и кривизной изогнутой оси бруса?

- Получите формулу нормальных напряжений при изгибе? Охарактеризуйте эпюру напряжений, величину наибольших нормальных напряжений, момента сопротивления сечения балки при изгибе?

- Получите формулу сдвигающей силы в продольных сечениях бруса при изгибе. Как используется эта формула при расчете составных сечений балок?

- Получите формулу касательных напряжений при из­гибе? Охарактеризуйте параметры, входящие в эту формулу, и постройте эпюры напряжений для прямоугольного и дву­таврового сечений бруса?

- Приведите формулировку и аналитическую запись условия прочности при изгибе?

- Покажите, как используется условие прочности при подборе сечения балки, определения допустимой величины изгибающего момента при заданном сечении балки, проверку прочности балки при заданной нагрузке?

- Как распределяются нормальные напряжения по поперечному сечению балки? В каких точках сечения они достигают наибольшего значения?

- Напишите формулу для определения нормального напряже­ния при изгибе в любой точке поперечного сечения?

- Напишите формулы для определения момента инерции и момента сопротивления для прямоугольника. Что характеризуют эти величины? Укажите единицы измерения этих величин?

- Напишите условие прочности при изгибе?

- Подберите размеры поперечного сечения балки в виде швелл­ера? Максимальный изгибающий момент 15кНм; допускаемое напряжение материала балки 160 МПа.

- Почему при поперечном изгибе в продольных сечениях балки возникают касательные напряжения?

- Каким опытом можно подтвердить возникновение касательных напряжений в продольных сечениях балки?

- Что представляет собой нейтральная линия сечения? Как определить ее положение?

- В каких точках поперечного сечения возникают при поперечном изгибе балки наибольшие касательные напряжения? Как их определить?

- Как составляют условие прочности балки при изгибе?

- Дифференциальные зависимости при изгибе.

- Правило знаков при построении эпюр.

- По какой формуле определяются нормальные напряжения в поперечных сечениях балки при поперечном изгибе?

- Сформулируйте теорему Д.И. Журавского?

- Какое напряжение в сечении балки вызывает поперечная сила?

- Какое напряжение в сечении балки вызывает изгибающий момент?

- Запишите формулу для определения касательных напряжений в поперечных сечениях балки при прямом поперечном изгибе?

- Как распределяются нормальные напряжения по высоте сечения балки?

- Как распределяются касательные напряжения по высоте сечения балки?

- Как записываются условия прочности при поперечном изгибе балки по нормальным напряжениям?

- Как записываются условия прочности при поперечном изгибе балки по касательным напряжениям?

- Какова разница в расчетах балок по допускаемой нагрузке и по допускаемым напряжениям?

- Как производится проверка прочности балки по главным напряжениям?

- Как определяется потенциальная энергия при поперечном изгибе?

- Как ведется расчет балок по разрушающей нагрузке?

- Какой вид имеют эпюры касательных напряжений в поперечных сечениях прямоугольной и двутавровой формы?

- Как находятся главные напряжения при изгибе?

- Как направлены главные площадки на уровне нейтрального слоя и в точках, наиболее удаленных от этого слоя?

- Что представляют собой траектории главных напряжений?

- Прогибы и углы поворота при изгибе.

- Какие формы поперечных сечений являются рациональными для балок из пластичных материалов?

- Какие перемещения получают поперечные сечения балок при прямом изгибе?

- Что называется упругой линией балки?

- Какие виды перемещений получают поперечные сечения балки при изгибе балок?

- Что называется прогибом балки?

- Какая зависимость между прогибами и углами поворо­та сечений балки?

- На основании каких соображений точное дифференци­альное уравнение прогибов балки заменяется приближенным?

- Выведите дифференциальное уравнение упругой линии балки?

- Сколько произвольных постоянных вводится при интегрировании уравнения прогибов и как они определяются?

- Запишите основное дифференциальное уравнение изогнутой оси балки.

- Какими величинами характеризуется при поперечном изгибе жесткость балки?

- Как записывается приближенное дифференциальное уравнение изогнутой оси балки?

- Что называют упругой линией балки?

- Какая зависимость существует между радиусом кривизны упругой линии , изгибающим моментом М _х и жесткостью балки EJ _x?

 

- Эпюры строят для нахождения опасных сечений?

1) да;

2) нет;

3) для определения законов изменения внутренних силовых факторов, напряжений и перемещений.

 

- Что опаснее при анализе эпюр изгиба?

1) максимальный изгибающий момент;

2) поперечная сила;

3) и то, и другое.

 

- Что означает скачок на эпюре моментов?

1) изменение сечения;

2) наличие сосредоточенного момента;

3) приложение сосредоточенной силы.

 

- Для двухопорной балки необходимо определить в начале реакции опор, а затем строить эпюры?

1) да;

2) нет;

3) это зависит от конструкции балки.

 

- Знак изгибающего момента не зависит от внешних сил?

1) нет;

2) да;

3) при наличии сосредоточенного момента.

 

- В поперечном сечении балки возникли изгибающий момент и поперечная сила. Укажите вид изгиба?

1) чистый изгиб;

2) поперечный изгиб.

 

- Изменится ли величина и знак поперечной силы и изгибающего момента, если они будут вычислены по внешним силам, расположенным слева или справа от сечения?

1) изменится;

2) не изменится.

 

- Поперечные силы в сечении на расстоянии z от концов балок выражены уравнениями: ; . Какими линиями очерчены эпюры поперечных сил?

1) в обоих случаях наклонными прямыми линиями;

2) в первом случае – прямой, параллельной оси балки, во втором – прямой, наклонной к оси балки.

 

- Изгибающие моменты в сечении на расстояние z от концов балок выражены уравнениями: 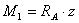; . Укажите какими линиями очерчены эпюры изгибающих моментов?

1) в обоих случаях наклонными прямыми линиями;

2) в первом случае – прямой, наклонной к оси, во второй – прямой, параллельной оси.

 

- Могут ли быть скачки на эпюре изгибающих моментов, если балка нагружена сосредоточенными силами и распределенной нагрузкой?

1) могут;

2) не могут.

 

- В каких единицах измеряется осевой момент инерции сечения?

1) м⁴;

2) м³;

3) м².

 

- Зависят ли значения нормальных напряжений от формы поперечных сечений балки?

1) зависит;

2) не зависит.

 

- Во сколько раз уменьшатся нормальные напряжения в прямоугольном сечении балки, если ее высота увеличится в два раза?

1) в два раза;

2) в четыре раза;

3) в восемь раз.

 

- По заданному изгибающему моменту при одинаковых допускаемых напряжениях были подобраны прямоугольные сечения балок в трех вариантах с разными соотношениями высоты h и ширины b: вариант I h: b =2; вариант II h: b =3; вариант III h: b =2,5. Какая из балок будет иметь наименьшую массу?

1) вариант I;

2) вариант II;

3) вариант III.

 

- Как изменится прогиб балки, если изгибающий момент уменьшить в три раза?

1) уменьшится в три раза;

2) уменьшится в шесть раз;

3) уменьшится в девять раз.

 

- Балки, изготовленные из стали и чугуна, имеющие одинаковые размеры и устройства опор, подвергаются действию одинаковых сил. сравните величину максимальных прогибов этих балок?

1) у стальной балки прогиб больше;

2) у чугунной балки прогиб больше;

3) прогиб балок одинаковый.

 

- Определите величину поперечной силы при изгибе данной балки.

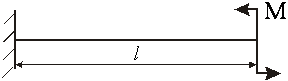
1. ;

2. ;

3. ;

4. .

 

- Какой вид деформации будет испытывать данная балка (см. рис. к предыдущему вопросу)?

1) поперечный изгиб;

2) продольно-поперечный изгиб;

3) чистый изгиб;

4) косой изгиб.

 

- Определите правильно построенную эпюру изгибающих моментов

- Укажите формулу для определения величины максимальных нормальных напряжений в опасном сечении балки

1) ;

2) ;

3) ;

4) .

 

- В какой из указанных точек возникают наибольшие нормальные напряжения?

 

- По какой формуле вычисляют нормальные напряжения в этой точке (см. рис. к предыдущему вопросу)?

1) ;

2) ;

3) ;

4) .

 

- В какой из указанных точек возникают наибольшие касательные напряжения?

 

- По какой формуле вычисляют касательные напряжения в этой точке (см. рис. к предыдущему вопросу)?

1) ;

2) ;

3) ;

4) .

 

- На рисунке показана балка, нагруженная внешними силами. Построены эпюры внутренних усилий. Укажите участок или участки, на которых возможно разрушение по нормальным напряжениям.

 

1) А-В;

2) В-С;

3) C-D;

4) A-D.

 

- Укажите участок или участки, на которых происходит деформация чистого изгиба (см. рис. к предыдущему вопросу)?

1) А-В;

2) В-С;

3) C-D;

4) A-D.

 

- На рисунке показана балка, нагруженная внешними силами. Построены эпюры внутренних усилий. Укажите участок или участки, на которых есть опасность разрушения по касательным напряжениям.

 

1) А-В;

2) В-С;

3) C-D;

4) A-D.

 

- Укажите участок или участки, на которых происходит деформация поперечного изгиба (см. рис. к предыдущему вопросу)?

1) А-В;

2) В-С;

3) C-D;

4) A-D.

 

- Условие прочности по нормальным напряжениям при чистом изгибе:

 

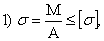
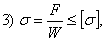
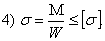
- Формула Журавского для определения касательного напряжения при поперечном изгибе:

 

- Чему равна поперечная сила в сечении бруса, в котором изгибающий момент достигает экстремальных значений?

1. Поперечная сила в этом сечении бруса равна нулю.

2. Поперечная сила в этом сечении бруса равна следующему значению .

3. Поперечная сила тоже достигает экстремальных значений.

4. Поперечную силу в данном случае можно определить по формуле Журавского.

⇐ Предыдущая15161718192021222324Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: