 |
Полная проверка прочности. Опасные сечения и опасные точки.
|
|
|
|
Для проверки на прочность при изгибе по действующим на балку внешним нагрузкам строят эпюры изменения внутренних усилий по ее длине и определяют опасные сечения балки, для каждого из которых необходимо провести проверку прочности.
При полной проверке прочности таких сечений будет, как минимум, три (иногда они совпадают):
1. сечение, в котором изгибающий момент М х - достигает своего максимального по модулю значения, - именно по этому сечению подбирают сечение всей балки;
2. сечение, в котором поперечная сила Q y, достигает своего максимального по модулю значения;
3. сечение, в котором и изгибающий момент М x и поперечная сила Q y достигают по модулю достаточно больших величин.
В каждом из опасных сечений необходимо, построив эпюры нормальных и касательных напряжений, найти опасные точки сечения (проверка прочности проводится для каждой из них), которых также будет, как минимум, три:
1. точка, в которой нормальные напряжения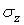 
, достигают своего максимального значения, - то есть точка на наружной поверхности балки наиболее удаленная от нейтральной оси сечения;
2. точка, в которой касательные напряжения 
достигают своего максимального значения, - точка, лежащая на нейтральной оси сечения;
3. точка, в которой и нормальные напряжения, и касательные напряжения, достигают достаточно больших величин (эта проверка имеет смысл для сечений типа тавра или двутавра, где ширина резко изменяет свое значение).
Пример 11.
Для заданных двух схем балок (рис.6.39) требуется написать выражения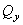 
, 
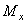для каждого участка в общем виде, построить эпюры 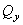, , 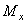найти 
и подобрать: для схемы а) деревянную балку круглого поперечного сечения при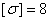 
МПа; для схемы б) стальную балку двутаврового поперечного сечения при 
МПа. При М = 20 кН/м, Р = 20 кН, q = 8 кН/м, 
м, 
м, 
, 
, 
.
|
|
|
А) б)
Рис.6.39
Решение.
А) б)
Рис.6.40
Схема а).
1. Для определения внутреннихусилий 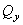, 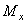используем метод сечений. Определим количество участков: граничными точками участков являются точки приложения сосредоточенных сил и моментов, а также точки начала и конца распределенной нагрузки. В данной задаче консольная балка имеет два участка. Рассечем последовательно со свободного конца каждый изних.Отбрасывая часть балки, включавшую защемление, определим внутренние силовые факторы в сечении. Поперечная сила равна алгебраической сумме проекций сил, приложенных к отсеченной части на поперечную ось (ось у), изгибаюший момент равен алгебраической сумме моментов, возникающих на отсеченной части относительно оси х в сечении. При определении знаков, используем следующее правило: поперечная сила положительна, если отсеченная часть стремится повернуться по часовой стрелке относительно, точки сечения, изгибающий момент положителен, если балка становится вогнутой.
Запишем выражения для внутренних силовых факторов и сосчитаемих значения в граничных точках участков (рис.6.40, а).
1 участок: 
м
кН;
.
, 
кН;
, 
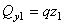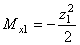кНм.
II участок: 
м
;
,
кН, 
кН;
кНм, 
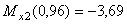кНм.
2. Построим эпюры внутренних силовых факторов, откладывая вычисленные значения на графике (рис.6.40, а). Соединим полученные точки прямыми линиями на участках, где аргумент z входит в первой степени и параболами, где z входит во второй степени. Таким образом, эпюра изгибающего момента на первом участке будет криволинейной, остальные участки эпюр будут прямолинейными. Определим опасное сечение балки, т.е. сечение, в котором изгибающий момент достигает наибольшего по модулю значения. Опасным сечением будет сечение на опоре, где 
кН/м.
3. Диаметр круглого сечения найдем из условия прочности
|
|
|
,
, 
,
м.
Схема б).
1. Для балки, лежащей на двух шарнирных опорах (рис.6.40, б), найдем опорные реакции RА, НА, RВ. Запишем уравнения равновесия статики:
;
;
.
;
.
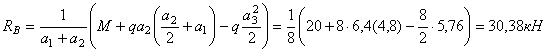Для проверки правильности определения реакций запишем еще одно уравнение равновесия, которое должно тождественно удовлетвориться при правильно найденных значениях реакций.
,
.
Балка имеет три участка, рассечем каждыйиз них.
I участок: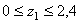 
кН;
.
, 
кН;
, 
кНм.
II участок: 
м
;
,
кН, 
кН;
, 
кНм.
2. Построим эпюры, соединяя полученные значения 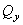и 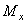. На втором участке эпюра 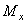имеет максимум при 
. Для определения величины максимального момента приравняем нулю выражение поперечной силы на участке, определим величину и подставим ее в выражение изгибающего момента:
,
м,
кНм.
Двутавровое сечение найдемиз условия прочности, определив необходимую величину момента сопротивления
,
.
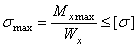Из сортамента прокатной стали (ГОСТ 8239-72) выберем двутавр с 
см3,
, 
см3.
|
|
|
