Определение напряжений при косом изгибе

Если разложить внешние силы по главным осям инерции Ох и Оу, то получим две системы сил P_1x, P_2x, …, P_nx и P_1y, P_2y,..., P_ny, каждая из.которых вызывает прямой изгиб с изгибающими моментами соответственно M_y и М_x (рис.7.6). Применяя принцип независимости действия сил, нормальные напряжения 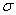(рис.7.7) определим как алгебраическую сумму напряжений от M_x и М_y:

Чтобы не связывать себя формальными правилами знаков, слагаемые будем определять по модулю, а знаки ставить по смыслу.

Таким образом, расчет на косой изгиб с применением принципа независимости действия сил сводится к расчету на два прямых изгиба с последующим алгебраическим суммированием напряжений.

Рис.7.6. Расчетная модель косого изгиба бруса

 

Рис.7.7. Связь нормального напряжения с внутренними изгибающими моментами

 

В случае поперечных сечений, имеющих две оси симметрии и выступающие угловые точки (рис.7.8) с равными по модулю и максимальными одноименными координатами и напряжения в этих точках будут равны

Слагаемые в этом выражении рекомендуется определять по модулю, а знаки ставить по смыслу. Например, на рис.7.9 верхний ряд знаков «+» и «—» соответствует напряжениям от М_x, а нижний ряд — от M_y, и напряжения в этих точках будут равны

 

Рис.7.8. Симметричные варианты сечений

 

 

Рис.7.9. Расстановка знаков от действия моментов

 

Условие прочности для балок из пластичного материала с указанным типом сечений запишется в виде

Касательные напряжения от поперечных сил, если нельзя воспользоваться формулой Журавского, допустимо не учитывать.

При проведении расчетов на прочность условие прочности составля­ется для опасной точки поперечного сечения, т.е. для точки, в которой нормальные напряжения достигают максимальных значений. Самой нагруженной точкой в сечении произвольной формы является точка, наиболее удаленная от нейтральной линии, разделяющей растянутую и сжатую зоны сечения.

В связи с этим, большое значение приобретают вопросы, связанные с определением положения нейтральной линии.

Положив , получим уравнение нейтральной линии.

Так как напряжения в точках поперечного сечения будут пропорциональными расстояниям от нейтральной линии, то max 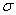будут возникать в наиболее удаленных от нее точках.

Силовая плоскость – это плоскость действия результирующего момента М _рез (рис.7.10), - угол наклона силовой плоскости к вертикали.

Рис.7.10

 

(1)

Свойства нейтральной линии

1. Если , то , то есть силовая плоскость и нейтральная линия не являются перпендикулярными.

2. Если , то из (1) следует, что , то есть нейтральная линия и силовая плоскость перпендикулярны. В этом случае стержень испытывает плоский изгиб (примерами таких стержней являются стержни с сечением – круг, кольцо, квадрат).

3. Знак «минус» в формуле (1) указывает, что силовая плоскость и нейтральная линия при косом изгибе проходят через противоположные квадранты.

Для определения опасных точек сечения следует построить касательные к контуру сечения, параллельные нейтральной линии. Точки касания и будут являться опасными (точк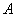и и на рис.7.11).

Рис.7.11. Положение нейтральной линии при косом изгибе

 

Для некоторых сечений (прямоугольник, двутавр, швеллер и т.п.) наиболее напряженные точки расположены в углах этих сечений, т.е. их можно найти без определения положения нейтральной линии (рис.7.12).

Рис.7.12. Положение нейтральной линии и опасных точек

сечения при косом изгибе для прямоугольника

 

Условия прочности составляют в зависимости от свойств того материала, из которого изготовлен элемент конструкции (брус).

Для хрупкого материала используют два условия прочности - для опасной точки, где имеет место растяжение (для нашего случая т. 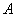на рис.7.11), и для точки, где имеет место сжатие (т. )

Необходимость использования двух условий прочности для хрупкого материала объясняется разными механическими свойствами материала при растяжении и сжатии. Хрупкий материал плохо сопротивляется растяжению и хорошо - сжатию.

Для пластичного материала, который одинаково сопротивляется и растяжению и сжатию, используют одно условие прочности для точки поперечного сечения, где имеют место максимальные по абсолютной величине нормальные напряжения

где и - координаты данной точки.

При расчетах на прочность касательными напряжениями от поперечных сил пренебрегают, т.к. их влияние незначительно.

 

 

⇐ Предыдущая15161718192021222324Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: