Примем следующий порядок расчета.

1. Разлагаем все внешние силы на составляющие

P_1x, P_2x,..., P_nx и P_1y, P_2y,..., P_ny.

2. Строим эпюры изгибающих моментов M_ч и M_y. от этих групп сил.

У кругового и кольцевого поперечного сечений все центральные оси главные, поэтому косого изгиба у вала вообще не может быть, следовательно, нет смысла в каждом сечении иметь два изгибающих момента M_x, и M_y, а целесообразно их заменить результирующим (суммарным) изгибающим моментом (рис.7.30)

,

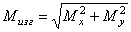который вызывает прямой изгиб в плоскости его действия относительно нейтральной оси п—п, перпендикулярной вектору М_изг. Эпюра суммарного момента имеет пространственное очертание и поэтому неудобна для построения и анализа. Поскольку все направления у круга с точки зрения прочности равноценны, то обычно эпюру М_изг спрямляют, помещая все ординаты в одну (например, вертикальную) плоскость. Обратим внимание на то, что центральный участок этой эпюры является нелинейным.

Рис.7.30

 

3. Строится эпюра крутящего момента М_z.. Эпюра крутящих моментов строится так же, как и при чистом кручении.

4. Находится опасное сечение вала.

Опасное сечение вала будем искать, как и прежде, по эпюрам внутренних усилий. При построении эпюр внутренних усилий при кручении с изгибом необходимо иметь ввиду следующие правила:

- эпюры крутящего момента M_x, а также эпюры составляющих поперечной силы Q_y, Q_z и изгибающего момента M_y, M_z строятся по той же процедуре, что и ранее;

- результирующая поперечная сила Q может не лежать в плоскости действия результирующего изгибающего момента M _и, а потому между ними уже не будет соблюдаться зависимость Журавского (dM/dx=Q), а, следовательно, и правила проверки эпюр, введенные для плоского изгиба;

- эпюра полного изгибающего момента будет прямой только на тех участках, где M_y и M_z ограничены прямыми с общей нулевой точкой, на участках, где такая общая точка отсутствует эпюра M _и будет описываться вогнутой кривой и строится по точкам (связано с тем, что вектор M _и в разных сечениях имеет различное направление).

Опасное сечение при кручении с изгибом устанавливается из совместного анализа эпюр крутящего M_x и полного изгибающего M _и моментов. Если в сечении вала постоянного диаметра с наибольшим изгибающим моментом М действует наибольший крутящий момент М _кр, то это сечение является опасным.

Если же такого явного совпадения нет, то опасным может оказаться сечение, в котором ни М ни М _крне являются наибольшими. Еще больше осложняется задача при валах переменного диаметра; у таких валов наиболее опасным может оказаться такое сечение, в котором действуют значительно меньшие изгибающие и крутящие моменты, чем в других сечениях.

В случаях, когда опасное сечение не может быть установлено непосредственно по эпюрам М и М _кр, необходимо проверить прочность вала в нескольких предположительно опасных сечениях.

5. После установления опасного сечения вала в нем находят опасные точки. В сечении возникают одновременно нормальные напряжения от изгибающего момента и касательные напряжения от крутящего момента и поперечной силы. В валах круглого сечения, длина которых во много раз больше диаметра, величины наибольших касательных напряжений от поперечной силы относительно невелики и при расчете прочности валов на совместное действие изгиба и кручения не учитываются.

Наибольшие напряжения изгиба возникают в точках k и k^/, наиболее удаленных от нейтральной оси (рис. 7.31),

.

где W_изг — момент сопротивления при изгибе.

В этих же точках имеют место и наибольшие касательные напряжения кручения

,

где W_р— момент сопротивления при кручении.

Рис.7.31

 

Как видно из рис. 7.31, в данном случае имеет место плоское напряженное состояние и расчет на прочность должен вестись по одной из гипотез прочности. Для пластичных материалов применяют гипотезу наибольших касательных напряжений (III) или энергетическую гипотезу (IV).

Условие прочности по III гипотезе записывается в виде

. (44)

В рассматриваемом случае

,

или

, (45)

где - эквивалентный момент по третьей гипотезе прочности.

Условие прочности по IV гипотезе прочности записывается в виде

. (46)

В рассматриваемом случае

,

или

, (47)

где - эквивалентный момент по четвертой гипотезе прочности.

Для хрупких материалов может быть использована гипотеза прочности Мора, которая для пластичных материалов приводится к третьей гипотезе, а для очень хрупких – к первой гипотезе

. (48)

Аналогичный расчет проводится и для кольцевого сечения.

Пример 9.

Стальной вал круглого поперечного сечения передает мощность N =14,7 кВт при угловой скорости =10,5 рад/с. Величина наибольшего изгибающего момента, действующего на вал M _и=1,5 кНм. Исходя из условий прочности по III и IV теориям прочности, определить необходимый диаметр вала, если =80 МПа.

Решение.

Условие прочности при одновременном действии изгиба и кручения по III гипотезе прочности

.

Находим величину передаваемого валом крутящего момента

.

Эквивалентный момент по третьей гипотезе прочности равен

а диаметр вала

,

или =63,5 мм.

Условие прочности при одновременном действии изгиба и кручения по IV гипотезе прочности

.

Эквивалентный момент по четвертой гипотезе прочности равен

,

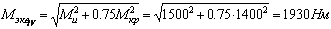а диаметр вала

,

или =62,3 мм.

Таким образом, расчет по энергетической теории прочности дал более экономичный размер сечения, чем по критерию наибольших касательных напряжений.

Вопросы для самопроверки

- Что такое сложное сопротивление стержней?

- Какие виды деформации бруса называют сложным со­противлением?

- Сформулируйте принципы, на которых строится рас­чет брусьев при сложном сопротивлении?

- В чем заключается принцип независимости действия сил?

- Опишите методику определения компонентов внутренних сил при сложном сопротивлении?

- Получите формулу нормальных напряжений при сложном сопротивлении?

- Дайте определение нулевой линии и опишите способы ее построения и эпюры нормальных напряжений при сложном сопротивлении?

- Какие внутренние усилия возникают в стержне в наиболее общем случае сложного сопротивления?

- Какой изгиб называется косым?

- Когда возникает косой изгиб? Опишите порядок расчета брусьев при косом изгибе?

- Сочетанием каких видов изгиба является косой изгиб?

- К каким равнодействующим приводятся внутренние силы при косом изгибе?

- По каким формулам определяются нормальные напряжения в поперечных сечениях балки при косом изгибе?

- Как находится положение нейтральной оси при косом изгибе?

- Как определяются опасные точки в сечении при косом изгибе?

- Как определяются перемещения точек оси балки при косом изгибе?

- Как определяется величина прогиба балки при косом изгибе?

- Как определить положение наиболее напряженной (опасной) точки бруса при косом изгибе?

Какие напряжения возникают в поперечном сечении бруса при изгибе с кручением?

- Как находятся опасные сечения бруса круглого сечения при изгибе с кручением?

- Какие напряжения испытывают вал и ось? Чем они принципиально отличаются?

- Какое напряженное состояние возникает в поперечном сечении вала при совместном действии изгиба и кручения?

- Какие напряжения возникают в поперечном сечении бруса при одновременном кручении и изгибе?

- Запишите выражения для эквивалентных моментов по различным гипотезам прочности, используемые при расчете бруса круглого сечения на прочность при одновременном изгибе и кручении?

- Напишите условие прочности для расчета вала?

- Как выбирается опасное сечение при расчете вала?

- Почему при изгибе с кручением и сочетании продольной силы с кручением расчет производится с использованием теорий прочности?

- В каких местах находятся опасные точки в брусе кругового сечения при сочетании продольной силы с кручением и изгиба с кручением?

- Получите выражения для главных напряжений в опасных точках при сочетаниях продольной силы с кручением и изгиба с кручением?

- Почему обычно не учитывают касательные напряжения от изгиба при расчете стержней на изгиб с кручением?

- Какие напряжения возникают в сечении вала в нагруженном состоянии?

- Какие теории прочности используются при расчете валов?

- Напишите расчетную формулу для определения диаметра вала?

На рисунке изображены различные поперечные сечения балок и положения плоскости действия изгибающих балку моментов. Ука­зать, в каких случаях будет плоский, в каких - косой изгиб?

1) 2) 3) 4)

 

- По какой формуле определяют напряжения при косом изгибе?

1) ;

2) ;

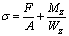3) ;

4) .

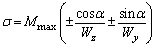- Какие точки данного поперечного сечения балки при косом изгибе будут опасными?

- Нейтральная ось при косом изгибе проходит:

1) перпендикулярно плоскости действия сил;

2) перпендикулярно плоскости прогибов;

3) перпендикулярно главной плоскости.

 

- Какой вид сложного сопротивления испытывает данный стержень?

1) Косой изгиб;

2) Изгиб и кручение;

3) Внецентренное растяжение-сжатие;

4) Продольный изгиб.

 

- Напряжения для данного стержня (см. рис. в предыдущем примере) в указанных точках определяют по формуле:

1) ;

2) ;

3) ;

4) .

 

- Определить в каком случае нормальные напряжения в основании стойки будут больше? Почему?

 

- Максимальные напряжения для стержня (а) (см. рис. в предыдущем примере) в основании стойки определяют по формуле:

1) ;

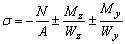2) ;

3) ;

4) .

 

- На валу, приводимом в движение мотором М, насажен посередине шкив весом 0,5 кН, диаметром 1,2 м. Натяжение ведущей части ремня, надетого на шкив, равно 0,6 кН, а ведомой - 0,3 кН. Какой вид сложного сопротивления испытывает вал:

1) внецентренное растяжение (сжатие);

2) косой изгиб;

3) изгиб с кручением;

4) изгиб с растяжением.

- Условие прочности для данного вала имеет вид:

1) ;

2) ;

3) ;

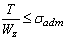4) .

 

- Какой вид сложного сопротивления испытывает вал зубчатой передачи?

1) изгиб с растяжением,

2) косой изгиб,

3) изгиб с кручением.

 

- Косой изгиб является сложным сопротивлением.

1) да;

2) нет;

3) да, если добавить растяжение- сжатие.

 

- Растяжение – сжатие вид сложного сопротивлении.

1) нет;

2) да;

3) да, в наклонном сечении стержня.

 

- При сложном сопротивлении, в каком случае в сечении имеются точки, где нормальное напряжение s равно нулю.

1) косой изгиб;

2) поперечный изгиб;

3) внецентренное растяжение- сжатие.

 

- При какой разновидности сложного сопротивления имеется «ядро сечение».

1) растяжение-сжатие;

2) изгиб с кручением;

3) внецентренное сжатие.

 

- Заклепочное соединение работает в условиях сложного сопротивления.

1) да;

2) нет;

3) при осевом сжатии заклепок.

 

 

 

 

⇐ Предыдущая15161718192021222324

Поделиться:

Воспользуйтесь поиском по сайту: