 |
Методы принятия сложных хозяйственных решений первого типа
|
|
|
|
В многокритериальной ситуации выбора, затрагивающей один РЦ хозяйственной системы, имеет место сложное хозяйственное решение первого типа.
Для разрешения ПС, связанных с первым типом сложных хозяйственных решений, применяются такие методы комплексного обоснования решений, как методы исследования операций.
Существо операционной задачи состоит в построении математической модели той ситуации, в которой требуется принять решение, а сама математическая модель представляет собой в общем случае описание некоторого комплексного показателя – критерия функционирования системы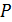 
– в его зависимости от управляемых переменных 
и неуправляемых параметров 
в данном хозяйственном звене.
Возникает задача объединить в один комплексный показатель 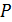несколько разнородных технико-экономических показателей 
(стоимость, трудоемкость, срок изготовления и т.д.) с учетом их значимости 
, т.е. построить формулу вида (31):
(31)
Коэффициенты рассматриваются как весовые коэффициенты, или коэффициенты значимости, учитывающие размерности и приводящие их к одной шкале. Другими словами, показатель общей эффективности 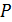является целевой функцией, отражающей интересы комплекса. При этом учитываются ограничения, налагаемые на переменные, представленные уравнениями и неравенствами.
Таким образом, рассмотренная выше задача оптимизации в ситуации простого хозяйственного решения выступает как частный случай общей модели комплексного анализа оценки и оптимизации сложного хозяйственного решения первого типа.
Если в случае простых хозяйственных решений структура целевой функции довольно проста – в качестве критерия оптимальности принимается естественная цель с естественной единицей измерения по данной цели (стоимость, прочность и т.д.), то в случае сложных хозяйственных решений возникает задача определения ценности (полезности) каждой цели из множества целей 
с позиций принятого комплексного критерия оптимальности, в качестве необходимого этапа выделяется определение (или предложение) способа сведения, вообще говоря, разнородных единиц измерения к одной. Другими словами, комплексный показатель общей эффективности 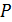является целевой функцией, отражающей «интересы» на множестве целей . Таким образом, при принятии сложных хозяйственных решений мы сталкиваемся с ситуацией, когда, с одной стороны, имеется возможность реализовать оптимизирующее поведение с позиции принятого комплексного критерия оптимальности в данном звене, а с другой стороны, структура этого комплексного критерия оптимальности требует применения той или иной схемы компромисса между частными целями общего критерия. Альтернатива, имеющая наибольшую (наименьшую) величину показателя общей эффективности 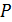, может рассматриваться как оптимальная на рассматриваемом множестве целей.
|
|
|
Наиболее распространенными формами свертки критериев являются следующие:
1. Аддитивный критерий. В этом случае в качестве обобщенного показателя 
принимается взвешенная сумма оценок альтернативы по отдельным частным целям 
(32):
(32)
2. Мультипликативный критерий. Обобщенный показатель эффективности строится как взвешенное произведение частных оценок альтернативы по отдельным целям (33).
(33)
Иногда находят применение и такие способы свертки, при которых каждое решение оценивается с точки зрения цели, степень достижения которой с учетом весового коэффициента является наибольшей или наименьшей (34, 35).
|
|
|
3. Конъюнктивный критерий:
(34)
4. Дизъюнктивный критерий:
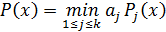(35)
Коэффициенты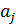 
характеризуют ценность соответствующего показателя с позиции принятого критерия оптимальности и выбираются исходя из степени важности отдельных целей. Особенностью этих коэффициентов является то, что они позволяют производить свертывание целевой функции с учетом неопределенности. В частности, обращение на практике к опыту и интуиции специалистов основано как раз на способности специалиста формировать комплексные оценки объектов с разнородными свойствами. Именно эта способность экспертов лежит в основе конструирования процедур экспертных оценок.
При формировании обобщенных критериев показателей существуют и специальные способы свертывания показателей по элементам риска и неопределенности. К такого рода сверткам относятся, например, критерии математического ожидания, критерий максимина, критерий Гурвица, Севиджа и др.
Принципиальной особенностью процесса многокритериального принятия решений является то, что, независимо от выбранного принципа оптимальности, оптимальное решение всегда принадлежит области компромиссов.
При принятии сложных хозяйственных решений в ситуации «одно звено – много критериев», наряду с моделями построения обобщенных критериев оптимизации, используются модели, основанные на выделении области компромиссов, оптимальных по Парето. Наиболее широко используется общая схема компромисса, или так называемая модель справедливого компромисса, при которой относительный уровень снижения качества по одному или нескольким критериям не превосходит относительного уровня повышения качества по другим критериям.
Рассмотрим подробней оптимальные по Парето решения. При принятии сложных решений, направленных на максимизацию (минимизацию) значений нескольких противоречащих друг другу критериев, отыскиваются так называемые Парето-оптимальные решения.
В. Парето в начале XX в. математически сформулировал один из самых распространенных критериев оптимальности, предназначенный для того, чтобы проверить, улучшает ли предложенное изменение в экономике общий уровень благосостояния.
|
|
|
Критерий Парето звучит следующим образом: «Следует считать, что любое изменение, которое никому не причиняет убытков и которое приносит некоторым людям пользу (по их собственной оценке), является улучшением».
На рисунке 35 точкой А показано исходное состояние экономической системы, состоящей из двух подсистем (группы X и Y). Улучшают его лишь те решения, которые приводят систему в любую точку, лежащую в заштрихованной области и на ее границах (например, точки B, C, D). Решение, обозначенное точкой E, не удовлетворяет требованию Парето, несмотря на значительный рост удовлетворения потребностей членов группы Y, потому что он достигается за счет снижения уровня благосостояния группы X.
Рис. 35. Оптимальность по Парето
|
|
|
