Условия использования процедур экспертизы

Широкое применение методов экспертных оценок вызвано практической необходимостью. В ряде областей экспертные методы оценки остаются практически единственными. Это привело к созданию целого ряда их самых разнообразных модификаций и оригинальных разработок.

Представляется целесообразным рассмотреть некоторые особенности и ограничения этих методов, выявившиеся в процессе их практического применения.

Само по себе присуждение оценок или весового коэффициента тем или иным событиям является субъективным и зависит от многих привходящих обстоятельств: способа построения и содержания таблиц экспертных оценок; количества вопросов, на которые должен дать ответ эксперт; его общей эрудиции и компетентности в данном круге вопросов; выбранной шкалы оценок, непосредственно от состояния эксперта в момент опроса и т.д.

Последующая процедура обработки этих оценок, их усреднение, сближение посредством специальных операций, повторных туров экспертизы, «отбрасывания» крайних мнений, может еще более усугубить определенную приблизительность этих оценок: класс точности количественных данных на выходе информационной системы не может превышать класс точности, с которой эти данные были заложены не ее входе. Очень часто это обстоятельство упускается из виду. Положение, при котором недостаточно надежная информация обрабатывается с помощью тонких и сложных математических методов, приводит к так называемым ошибкам второго рода.

Обработка «хорошей» информации «плохими» методами также существенно влияет на эффективность решения, приводя к ошибкам первого рода.

Поэтому совершенствование методов экспертных оценок предполагает, с одной стороны, разработку аппарата, позволяющего более совершенно присуждать сами оценки, т.е. уточнять входные данные, с другой стороны, требует постоянного внимания к математическому аппарату, используемому для обработки экспертных оценок.

Для получения работоспособного или близкого к оптимальному решения в рассматриваемых условиях необходима разработка и применение системы выбора решения, позволяющей сочетать знания, опыт, интуицию специалистов (руководителей), их субъективные суждения и математические методы, дающие способы «объективизации» этих субъективных суждений и представление данных в наиболее целесообразной и полезной форме.

Разработка и применение методов экспертных оценок, безусловно, является необходимой и перспективной, так как они являются, по существу, единственными методами решения хозяйственных задач, когда алгоритм неизвестен в принципе. Они являются также незаменимыми в случае ограниченного времени на решение задачи даже при наличии известного алгоритма.

 

Вопросы и задания для самоконтроля

1. Перечислите основные этапы процедуры многомерной экспертизы.

2. Раскройте суть процедуры Электра.

3. Назовите достоинства и недостатки экспертных методов.

4. Охарактеризуйте «ошибки первого рода».

5. Охарактеризуйте «ошибки второго рода».

 

Тема 5. Принятие решений на основе метода анализа иерархий Т. Саати

Метод анализа иерархий

В этой теме излагается теория, предложенная Т. Саати в [11], применение которой сводит исследование даже очень сложных систем к последовательности попарных сравнений соответствующим образом определенных компонент.

Данный метод можно описать следующим образом. Допустим, заданы элементы определенного уровня иерархии и один элемент 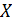 следующего, более высокого уровня. Нужно сравнить элементы данного уровня попарно по силе их влияния на 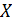, поместить числа, отражающие достигнутое при сравнении согласие во мнениях, в матрицу и найти собственный вектор с наибольшим собственным значением. Собственный вектор обеспечивает упорядочение приоритетов, а собственное значение является мерой согласованности суждений.

Определим шкалу приоритетов для следующего примера. Пусть A, B, С и D обозначают стулья, расставленные по прямой линии, ведущей от источника света. Создадим шкалу приоритетов относительной освещенности для стульев. Суждения производит человек, стоящий около источника света, у которого, например, спрашивают: «Насколько сильнее освещенность стула B по сравнению с C?» Он отвечает одним из чисел, и это суждение заносится в позицию (В, С) матрицы. По соглашению, сравнение силы всегда производится для действия или объекта, стоящего в левом столбце, по отношению к действию или объекту, стоящему в верхней строке. Мы имеем матрицу попарных сравнений для четырех строк и четырех столбцов (табл. 25).

Таблица 25 – Матрица попарных сравнений

Освещенность	A	B	C	D
A
B
C
D

Условимся по поводу чисел, которые заносятся в матрицу. Пусть заданы элементы A и B; если:

• A и B одинаково важны, заносим 1 в позицию (А, В), где пересекаются строка A и столбец В;

• A незначительно важнее, чем B, заносим 3;

• A значительно важнее B, заносим 5;

• A явно важнее B, заносим 7;

• A по своей значительности абсолютно превосходит B, заносим 9.

При сравнении элемента с самим собой имеем равную значительность, так что на пересечении строки A со столбцом A в позиции (А, А) заносим 1. Поэтому главная диагональ матрицы должна состоять из единиц. Заносим соответствующие обратные величины: 1, 1/3, 1/5, 1/7, 1/9 на пересечениях столбца A и строки B, т. е. в позицию (В, A) для обратного сравнения B с A. Числа 2, 4, 6, 8 и их обратные величины используются для облегчения компромиссов между слегка отличающимися от основных чисел суждениями.

В общем случае, под согласованностью подразумевается то, что при наличии основного массива необработанных данных все другие данные логически могут быть получены из них.

Для проведения парных сравнений n объектов или действий при условии, что каждый объект или действие представлены в данных, по крайней мере, один раз, требуется (n −1) суждений о парных сравнениях.

Насколько плоха согласованность для определенной задачи, можно оценить путем сравнения полученного нами значения величины (λmax – n) / (n −1) с ее значением из случайно выбранных суждений и соответствующих обратных величин матрицы того же размера.

Вернемся теперь к нашему примеру освещенности стульев. В матрице для чисел имеется 16 полей. Четыре из них уже определены, а именно те, что находятся на диагонали, (А, А), (В, В), (C, C), (D, D) и равны единице, так как, например, стул A имеет одинаковую освещенность по отношению к самому себе. Для оставшихся после заполнения диагонали 12-ти чисел нужно провести шесть сравнений, поскольку остальные шесть являются обратными сравнениями и их оценки должны быть обратными величинами к оценкам первых шести. Допустим, что человек, используя рекомендованную шкалу, вносит число 4 в позицию (В, С), так как полагает, что интенсивность освещенности стула B по сравнению со стулом C находится между слабой и сильной. Тогда в позицию (С, В) автоматически заносится обратная величина, т. е. 1/4, что не обязательно, но в общем случае рационально. После проведения оставшихся пяти суждений, а также занесения их обратных величин для всей матрицы получим таблицу 26.

Таблица 26 – Заполненная матрица парных сравнений

Освещенность	A	B	C	D
A	1	5	6	7
B	1/4	1	4	6
C	1/6	1/4	1	4
D	1/7	1/6	1/4	1

Следующий шаг состоит в вычислении вектора приоритетов по данной матрице. В математических терминах это – вычисление главного собственного вектора, который после нормализации становится вектором приоритетов.

В отсутствие компьютера, позволяющего точно решить данную задачу, можно получить грубые оценки вектора приоритетов следующими четырьмя способами, которые представлены ниже в порядке увеличения точности оценок.

1. Суммировать элементы каждой строки и нормализовать делением каждой суммы на сумму всех элементов; сумма полученных результатов будет равна единице. Первый элемент результирующего вектора будет приоритетом первого объекта, второй – второго объекта и т. д.

2. Суммировать элементы каждого столбца и получить обратные величины этих сумм. Нормализовать их так, чтобы их сумма равнялась единице, разделить каждую обратную величину на сумму всех обратных величин.

3. Разделить элементы каждого столбца на сумму элементов этого столбца (т. е. нормализовать столбец), затем сложить элементы каждой полученной строки и разделить эту сумму на число элементов строки. Это процесс усреднения по нормализованным столбцам.

4. Умножить n элементов каждой строки и извлечь корень n-й степени. Нормализовать полученные числа.

Приведем метод получения грубой оценки согласованности. Умножив матрицу сравнений справа на полученную оценку вектора решения, получим новый вектор. Разделив первую компоненту этого вектора на первую компоненту оценки вектора решения, вторую компоненту нового вектора на вторую компоненту оценки вектора решения и т. д., определим еще один вектор. Разделив сумму компонент этого вектора на число компонент, найдем приближение к числу λ max (называемому максимальным, или главным, собственным значением), используемому для оценки согласованности, отражающей пропорциональность предпочтений. Чем ближе λmax к n (числу объектов или видов действия в матрице), тем более согласован результат.

Отклонение от согласованности может быть выражено величиной (λmax − n)/ (n −1), которую назовем индексом согласованности (ИС).

Индекс согласованности сгенерированной случайным образом по шкале от 1 до 9 обратно-симметричной матрицы с соответствующими обратными величинами элементов, назовем случайным индексом (СИ).

Ниже представлены порядок матрицы (первая строка) и средние СИ (вторая строка), определенные так, как описано выше (табл. 27).

Таблица 27 – Случайные индексы для матриц различных порядков

Порядок матрицы	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
СИ	0,00	0,00	0,58	0,90	1,12	1,24	1,32	1,41	1,45	1,49	1,51	1,48	1,56	1,57	1,59

Отношение ИС к среднему СИ для матрицы того же порядка называется отношением согласованности (ОС). Значение ОС, меньшее или равное 0,10, будем считать приемлемым.

Чтобы проиллюстрировать на примере наши приближенные вычисления ИС, для нахождения λmax используем приведенную выше матрицу и третий вектор-столбец, полученный методом 3. После умножения матрицы справа на вектор приоритетов (0,59; 0,25; 0,11; 0,05), имеем вектор-столбец (2,85; 11,11; 0,47; 0,20). Разделив компоненты этого вектора на соответствующие компоненты первого вектора, получим (4,83; 4,44; 4,28; 4,00), а в результате усреднения последних – λ max = 4,39. Отсюда ИС = (4,39-4)/3=0,13. Для определения того, насколько хорош этот результат, разделим его на соответствующий СИ = 0,90. Отношение согласованности (ОС): 0,13/0,90 = 0,14, что, пожалуй, не так уж близко к 0,10.

Эти сравнения и вычисления устанавливают приоритеты элементов некоторого уровня иерархии относительно одного элемента следующего уровня. Если уровней больше, чем два, то различные векторы приоритетов могут быть объединены в матрицы приоритетов, из которых определяется один окончательный вектор приоритетов для нижнего уровня.

 

Предыдущая14151617181920212223242526272829Следующая

Поделиться:

Воспользуйтесь поиском по сайту: