 |
Пример иерархической композиции приоритетов
|
|
|
|
Задача о выборе школы
Был проведен анализ трех школ А, В и С на предмет их желательности с точки зрения сына автора методики. Для сравнения были выбраны шесть независимых характеристик: учеба, друзья, школьная жизнь, профессиональное обучение, подготовка к колледжу и обучение музыке (рис. 37). Полученные матрицы попарных сравнений показаны в табл. 28 и 29.
Рис. 37. Иерархия удовлетворения школой
Таблица 28 – Сравнение характеристик относительно общего удовлетворения школой
| Учеба | Друзья | Школьная жизнь | Проф. обучение | Подготовка к колледжу | Обучение музыке | |
| Учеба | 1 | 4 | 3 | 1 | 3 | 4 |
| Друзья | 1/4 | 1 | 7 | 3 | 1/5 | 1 |
| Школьная жизнь | 1/3 | 1/7 | 1 | 1/5 | 1/5 | 1/6 |
| Проф. обучение | 1 | 1/3 | 5 | 1 | 1 | 1/3 |
| Подготовка к колледжу | 1/3 | 5 | 5 | 1 | 1 | 3 |
| Обучение музыке | 1/4 | 1 | 6 | 3 | 1/3 | 1 |
.
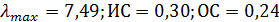Таблица 29 – Сравнение школ относительно шести характеристик
| Учеба | А | В | С | Друзья | А | В | С | |
| А | 1 | 1/3 | 1/2 | А | 1 | 1 | 1 | |
| В | 3 | 1 | 3 | В | 1 | 1 | 1 | |
| С | 2 | 1/3 | 1 | С | 1 | 1 | 1 | |
| λmax=3,05 | λmax=3,00 | |||||||
| ИС=0,025 | ИС=0 | |||||||
| ОС=0,024 | ОС=0 |
| Школьная жизнь | А | В | С | Проф. Обучение | А | В | С | |
| А | 1 | 5 | 1 | А | 1 | 9 | 7 | |
| В | 1/5 | 1 | 1/5 | В | 1/9 | 1 | 1/5 | |
| С | 1 | 5 | 1 | С | 1/7 | 5 | 1 | |
| λmax=3,00 | λmax=3,21 | |||||||
| ИС=0 | ИС=0,105 | |||||||
| ОС=0 | ОС=0,18 |
| Подготовка к колледжу | А | В | С | Обучение музыке | А | В | С | |
| А | 1 | 1/2 | 1 | А | 1 | 6 | 4 | |
| В | 2 | 1 | 2 | В | 1/6 | 1 | 1/3 | |
| С | 1 | 1/2 | 1 | С | 1/4 | 3 | 1 | |
| λmax=3,00 | λmax=3,05 | |||||||
| ИС=0 | ИС=0,025 | |||||||
| ОС=0 | ОС=0,04 |
Таблица 30 – Коэффициенты значимости признаков
| Коэффициенты \ Признаки | Учеба | Друзья | Школьная жизнь | Проф. обучение | Подготовка к колледжу | Обучение музыке |
| 0,16 | 0,33 | 0,45 | 0,77 | 0,25 | 0,69 |
| 0,59 | 0,33 | 0,09 | 0,05 | 0,50 | 0,09 |
| 0,25 | 0,33 | 0,46 | 0,17 | 0,25 | 0,22 |
Вектор приоритетов первой матрицы (табл. 28) получается равным (0,32; 0,14; 0,03; 0,13; 0,24; 0,14), и соответствующее ему собственное значение 
, что достаточно далеко от значения в случае согласованности, равного 6; ИС = 0,30 и ОС = 0,30/1,24 = 0,24, что также достаточно велико.
|
|
|
Чтобы получить общее ранжирование школ, умножим матрицу табл. 30 справа на транспонированный вектор-строку весов характеристик. Это то же самое, что взвесить каждый из полученных выше шести собственных векторов приоритетом соответствующей характеристики и затем сложить (что допустимо при независимости характеристик). В результате имеем: А = 0,37; В = 0,38; С = 0,25.
Сын автора методики поступил в школу А, так как она получила почти такую же оценку, что и школа В, и была бесплатной, в отличие от частной школы В.
Объяснение рис. 37. Критерии на рисунке обозначены через У, Д, Ш, П, К и М. Если веса критериев и веса школ относительно каждого критерия такие, как обозначено вдоль каждого отрезка на рисунке 37, то общие оценки школ рассчитываются по формулам 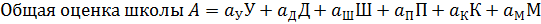(37):
.
. (37)
.
Предыдущие вычисления могут быть представлены в виде следующего матричного произведения:
Для выявления меры удовлетворения кандидата школой сначала следует перечислить важнейшие критерии, характеризующие школы, и вычислить сравнительную желательность этих критериев для кандидата. Желательность будет меняться от одного кандидата к другому. Например, для одного ученика друзья более привлекательны, чем подготовка к колледжу, в то время как другой ученик имеет противоположное мнение.
Следующим шагом является вычисление относительного ранга каждой школы по каждому критерию. Например, в одной школе лучше обучают музыке тогда, как другая школа славится профессиональным обучением.
Для получения общей оценки каждой школы нужно, во-первых, умножить вес оценки этой школы по некоторому критерию на вес этого критерия. Затем следует сложить значения, полученные для каждой школы, по всем критериям. Например, для школы А 
есть относительный вес учебы в этой школе. Так как относительный вес учебы есть У, общий вес учебы для школы А будет 
. Таким же образом вычисляем 
. Следовательно, общая оценка школы А будет суммой общих весов упомянутых видов деятельности, т.е. общая оценка школы А будет найдена по формуле:
|
|
|
.
Интересно посмотреть, как выглядели приоритеты три года спустя (табл. 31).
Таблица 31 – Общее удовлетворение школой три года спустя
| Учеба | Друзья | Школьная жизнь | Проф. обучение | Подготовка к колледжу | Обучение музыке | |
| Учеба | 1 | 5 | 7 | 5 | 3 | 1 |
| Друзья | 1/5 | 1 | 3 | 1/5 | 1/6 | 1/6 |
| Школьная жизнь | 1/7 | 1/3 | 1 | 1/4 | 1/5 | 1/5 |
| Проф. обучение | 1/5 | 5 | 4 | 1 | 1/5 | 1/6 |
| Подготовка к колледжу | 1/3 | 6 | 5 | 5 | 1 | 1 |
| Обучение музыке | 1 | 6 | 5 | 6 | 1 | 1 |
.
Соответствующий собственный вектор – (0,33; 0,05; 0,03; 0,09; 0,23; 0,27). Молодой человек (в 18 лет) больше не считает, что друзья или профессиональное обучение так важны. Его интерес к колледжу и музыке представляется преобладающим. Колледж и музыка стали для него насущной потребностью, а не отдаленными стремлениями.
Согласованность также очень повысилась. Приоритеты школ относительно характеристик получились теми же, что и раньше, и сейчас намного яснее, что тогда был сделан правильный выбор. Приоритеты школ следующие: А=0,40; В=0,36; С=0,25.
Вопросы и задания для самоконтроля
1. Раскройте суть метода парных сравнений.
2. Что понимается под согласованностью суждений?
3. Как вычислить индекс согласованности (ИС) и отношение согласованности (ОС)?
4. Какие можно сделать выводы на основе полученного значения показателя ОС?
СПИСОК ЛИТЕРАТУРЫ
1. Ваганов П.И. Управление организационными изменениями: основы инновационного управления и управленческих инноваций. Учебное пособие. – СПб.: Изд-во СПбГУЭФ, 2004. – 96 с.
2. Дедов Л.А., Тонких А.С., Эйсснер Ю.Н. К обоснованию метода эталонных темповых порядков. Открытый доступ: http://viperson.ru/uploads/attachment/file/949892/____________________.pdf (посетила 29.04.17)
3. Захарченко Н.Н. Экономические измерения: теория и методы. – СПб.: Изд-во СПбГУЭФ, 1993. –157с.
4. Исследование систем управления и системный анализ: Учеб. пособие. Ч.1: Методологические и методические основы / Н.В. Минеева, М.С. Мотышина, Н.Н. Погостинская, Ю.Н. Эйсснер; Под ред. М.С. Мотышиной. – Санкт-Петербург: Изд-во СПбГУЭФ, 2000. – 168 с.
|
|
|
5. Месарович М., Такахара Я. Общая теория систем: математические основы. – М: Издательство «Мир», 1978. – 311 с.
6. Мотышина М.С. Системный анализ: учеб. пособие. – Санкт-Петербург: Изд-во СПбГУЭФ, 2007. – 188 с.
7. Наследов А.Д. Математические методы психологического исследования. Анализ и интерпретация данных. Учебное пособие. 3-е изд., стереотип. – СПб: Речь, 2008. – 392 с.
8. Осипов А.К., Эйсснер Ю.Н. Моделирование и оценка динамики региональных экономических структур. Препринт. – Екатеринбург: ИЭ УрО РАН, 1996 г.
9. Отраслевые методические рекомендации по нормативной системе показателей эффективности и качества: Алгоритмическое обеспечение нормативной системы показателей / Захарченко Н.Н., Соломенко Н.Г.; рук.: Сыроежин И.М. – Таллин: [б. и.], 1977. – 23 с.
10. Погостинская Н.Н., Погостинский Ю.А. Системный подход в экономико-математическом моделировании: Учебное пособие. – СПб.: Изд-во СПбГУЭФ, 1999. – 74 с.
11. Саати Т. Принятие решений. Метод анализа иерархий. Перевод с английского Р.Г. Вачнадзе. – М.: «Радио и связь», 1993. – 278 с.
12. Сио К.К. Управленческая экономика. Пер. с англ. – М: Инфра-М, 2000. – 671 с.
13. Соколовская М.Б. Системная реструктуризация предприятия: теоретико-методологические. – СПб.: Изд-во СПбГУЭФ, 2001. – 151 с.
14. Сыроежин И.М. Планомерность. Планирование. План. – Москва: Экономика, 1986. – 248 с.
15. Сыроежин И.М. Сложные хозяйственные решения: теория и методы: учеб.пособие / Сыроежин И.М., Попова Т.Г., Эйсснер Ю.Н. – Ленинград: ЛФЭИ, 1979. – 75 с.
16. Сыроежин И.М. Экономическая кибернетика. Системный метод: учеб.пособие / И.М. Сыроежин, Т.Г. Попова, Ю.Н. Эйсснер. – Ленинград: [б. и.], 1977. – 67 с.
17. Сыроежин И.М. Основные системные признаки общественного хозяйства: учеб.пособие. – Ленинград: [б. и.], 1979. – 85 с.
18. Трофимова Л.А. Управленческие решения: методол. аспекты / Л.А. Трофимова, В.В. Трофимов. – Санкт-Петербург: Изд-во СПбГУЭФ, 2000. – 87 с.
19. Измерения в процессах моделирования социально-экономических систем. Часть 1. – Л.: Изд-во ЛФЭИ, 1991. – 103 с.
|
|
|
20. Измерения в процессах моделирования социально-экономических систем. Часть 2. – Л.: Изд-во ЛФЭИ, 1991. – 88 с.
21. Шелобаев С.И. Математические методы и модели в экономике, финансах, бизнесе: Учеб.пособие для вузов по экон.специальностям. – Москва: Юнити-Дана, 2000. – 367с.
22. Эйсснер Ю.Н. Организационно-экономические измерения в планировании и управлении. – Л.: Изд-во Ленинградского гос. ун-та, 1988. – 144 с.
23. Экономическая кибернетика: учеб.пособие. Ч. 1: Основы теории хозяйственных систем / отв. ред.: И.М. Сыроежин. – Ленинград: Изд-во Ленингр. ун-та, 1974. – 126 с.
24. Экономическая кибернетика: учеб.пособие. Ч. 2: Прикладные методы / Забежинская Е.Б. и др.; под ред. Сыроежина И.М. – Ленинград: [б. и.], 1973. – 175 с.
25. Экономическая кибернетика: учеб.пособие. Ч. 4: Основы системного анализа / Т.Г. Попова, И.М. Сыроежин (рук.), Ю.Н. Эйсснер; отв. ред.: И.М. Сыроежин. – Ленинград: [б. и.], 1976. – 135 с.
26. Янг С. Системное управление организацией. Пер. с англ. под ред. С.П. Никанорова, С.А. Батасова. – М.: «Советское радио», 1972. – 456 с.
27. Linton C. Freeman, Stephen P. Borgatti and Douglas R. White. Centrality in valued graphs: A measure of betweenness based on network flow // Social Networks, 13 (1991), pp. 141-154. Available at: http://moreno.ss.uci.edu/54.pdf (accessed 30.01.2017)
28. Matthew O. Jackson. Social and Economic Networks. Princeton University Press, 2008, 648 p. Available at: http://press.princeton.edu/titles/8767.html (accessed 30.01.2017)
29. Philip Bonacich. Power and Centrality: A Family of Measures // American Journal of Sociology, Vol. 92, No. 5 (Mar., 1987), pp. 1170-1182. Available at: http://www.leonidzhukov.net/hse/2014/socialnetworks/papers/Bonacich-Centrality.pdf (accessed 30.01.2017)
|
|
|
